NCERT Solutions For Class 6 Maths Algebra Exercise 11.5
NCERT Solutions For Class 6 Maths Algebra Exercise 11.5
NCERT Solutions For Class 6 Maths Chapter 11 Algebra Ex 11.5
Exercise 11.5
Ex 11.5 Class 6 Maths Question 1.
State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t – 7) > 5
(c) 4/2 = 2
(d) (7 x 3) – 19 = 8
(e) 5 x 4 – 8 = 2x
(f) x -2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 x 5) – (12 x 4)
(j) 7 = (11 x 2) + p
(k) 20 = 5y
(l) 3q/2 < 5 (m) z + 12 > 24
(n) 20 – (10 – 5) = 3 x 5
(o) 7 – x = 5
Solution:
(a) 17 = x + 7 is an equation with a variable x.
(b) (t – 7) > 5 is not an equation because it does not have ‘=’ sign.
(c) 4/2 = 2 is not an equation because it has no variable.
(d) (7 x 3) – 19 = 8 is not an equation because it has no variable.
(e) 5 x 4 – 8 = 2x is an equation with a variable x.
(f) x – 2 = 0 is an equation with a variable x.
(g) 2m < 30 is not an equation because it does not have ‘=’ sign.
(h) 2n + 1 = 11 is an equation with a variable n.
(i) 7 = (11 x 5) – (12 x 4) is not an equation because it does not have a variable.
(j) 7 = (11 x 2) + p is an equation with a variable p.
(k) 20 = 5y is an equation with a variable y.
(l) 3q/2 < 5 is not an equation because it does not have ‘=’ sign. (m) z + 12 > 24 is not an equation because it does not have ‘=’ sign.
(n) 20 – (10 – 5) = 3 x 5 is not an equation because it has no variable.
(o) 7 – x = 5 is an equation with a variable x.
Ex 11.5 Class 6 Maths Question 2.
Complete the entries in the third column of the table.
| S. No. | Equation | Value of variable | Equations satisfied Yes /No |
| (a) | 10y = 80 | y = 10 | |
| (b) | 10y = 80 | y = 8 | |
| (c) | 10y = 80 | y = 5 | |
| (d) | 4l = 20 | l = 20 | |
| (e) | 4l = 20 | l = 80 | |
| (f) | 4l = 20 | l = 5 | |
| (g) | b + 5 = 9 | b = 5 | |
| (h) | b + 5 = 9 | b = 9 | |
| (i) | b + 5 = 9 | b = 4 | |
| (J) | h – 8 = 5 | h = 13 | |
| (k) | h – 8 = 5 | h = 8 | |
| (l) | h – 8 = 5 | h = 0 | |
| (m) | P + 3 = 1 | p = 3 | |
| (n) | p + 3 = 1 | p = 1 | |
| (o) | p + 3 = 1 | p = 0 | |
| (P) | p + 3 = 1 | p = -1 | |
| (q) | p + 3 = 1 | p = -2 |
Solution:
| S. No. | Equation | Value of variable | Equations satisfied Yes /No |
| (a) | 10y = 80 | y = 10 | No |
| (b) | 10y = 80 | y = 8 | Yes |
| (c) | 10y = 80 | y = 5 | No |
| (d) | 4l = 20 | l = 20 | No |
| (e) | 4l = 20 | l = 80 | No |
| (f) | 4l = 20 | l = 5 | Yes |
| (g) | b + 5 = 9 | b = 5 | No |
| (h) | b + 5 = 9 | b = 9 | No |
| (i) | b + 5 = 9 | b = 4 | Yes |
| (J) | h – 8 = 5 | h = 13 | Yes |
| (k) | h – 8 = 5 | h = 8 | No |
| (l) | h – 8 = 5 | h = 0 | No |
| (m) | P + 3 = 1 | p = 3 | No |
| (n) | p + 3 = 1 | p = 1 | No |
| (o) | p + 3 = 1 | p = 0 | No |
| (P) | p + 3 = 1 | p = -1 | No |
| (q) | p + 3 = 1 | p = -2 | Yes |
Ex 11.5 Class 6 Maths Question 3.
Pick out the solution from the values given in the brackets next to each equation. Show that the other values do not satisfy the equation.
(а) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, -5)
(d) q/2 = 7 (7, 2, 10, 14)
(e) r – 4 = 0 (4, -4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
Solution:
(a) For m = 10, LHS = 5 x 10 = 50, RHS = 60
Here, LHS ≠ RHS
∴ m = 10 is not the solution of the equation
For m = 5, LHS = 5×5 = 25, RHS = 60
Here, LHS ≠ RHS
∴ m = 5 is not the solution of the equation
For m = 12, LHS = 5 x 12 = 60, RHS = 60
Here, LHS = RHS
∴ m = 12 is the solution of the equation
For m = 15 LHS = 5 x 15 = 75, RHS = 60
Here, LHS ≠ RHS
∴ m = 15 is not the solution of the equation
(b) n + 12 = 20 (12, 8, 20, 0)
For n = 12, LHS = 12 + 12 = 24, RHS = 20
Here, LHS ≠ RHS
∴ n = 12 is not the solution of the equation
For n = 8, LHS = 8 + 12 = 20, RHS = 20
Here, LHS = RHS
∴ n = 8 is the solution of the equation
For n = 20, LHS = 20 + 12 = 32, RHS = 20
Here, LHS ≠ RHS
∴ n = 20 is not the solution of the equation
For n = 0, LHS = 0 + 12 – 12, RHS = 20
Here, LHS ≠ RHS
∴ n= 0 is not the solution of the equation
(c) p – 5 = 5 (0, 10, 5, -5)
For p = 0, LHS = 0 – 5 = -5, RHS = 5
Here, LHS ≠ RHS
∴ p = 0 is not the solution of the equation
For p = 10, LHS = 10 – 5 = 5, RHS = 5
Here, LHS = RHS
∴ p = 10 is the solution of the equation
For p = 5, LHS = 5-5-0, RHS = 5
Here LHS ≠ RHS
∴ p = 5 is not the solution of the equation
For p = 5, LHS = 5 – 5 = 0, RHS = 5
Here, LHS ≠ RHS
∴ p = -5 is not the solution of the equation

(e) r – 4 = 0 (4, -4, 8, 0)
For r = 4, LHS = 4 – 4 = 0, RHS = 0
Here, LHS = RHS
∴ r = 4 is the solution of the equation
For r = -4, LHS = -4 – 4 = -8, RHS = 0
Here, LHS ≠ RHS
∴ r = -4 is not the solution of the equation
For r = 8, LHS = 8 – 4 = 4, RHS = 0
Here, LHS ≠ RHS
For r = 8 is not the solution of the equation
For r = 0, LHS = 0 – 4 = – 4, RHS = 0
Here, LHS ≠ RHS
∴ r = 0 is not the solution of the equation
(f) x + 4 = 2 (-2, 0, 2, 4)
For x = -2, LHS = -2 + 4 = 2, RHS = 2
Here, LHS – RHS
∴ x = -2 is the solution of the equation
For x = 0, LHS = 0 + 4 – 4, RHS = 2
Here, LHS ≠ RHS
∴ x = 0 is not the solution of the equation
For x = – 2, LHS = -2 + 4 – 6, RHS = 2
Here, LHS ≠ RHS
∴ x = 2 is not the solution of the equation
For r = 4, LHS = 4 + 4 = 8, RHS = 2
Here, LHS ≠ RHS
∴ x = 4 is not the solution of the equation
Ex 11.5 Class 6 Maths Question 4.
(a) Complete the table and by inspection of the table find the solution to the equation m + 10 = 6

(b) Complete the table and by inspection of the table find the solution to the equation 51 – 35

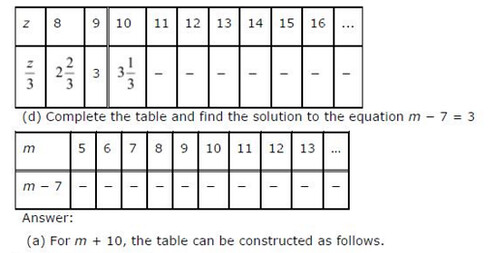
(c) Complete the table and find the solution of the equation g = 4 using the table.

(d) Complete the table and find the solution to the equation m – 7 = 3

Solution:
(a) By inspections, we have

So, m – 6 is the solution of the equation.
(b) Given that 5t = 35

So, t = 7 is the solution of the equation.
(c) Given that z/3 = 35

So, z = 12 is the solution of the equation.
(d) Given that m – 7 = 3

So, m = 10 is the solution of the equation.
Ex 11.5 Class 6 Maths Question 5.
Solve the following riddles, you may yourself construct such riddles. Who am I?
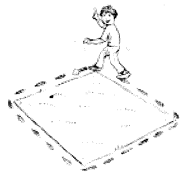
(i) Go round a square
Counting every corner
Thrice and no more!
Add the count to me
To get exactly thirty four!
(ii) For each day of the week
Make an upcount from me
If you make no mistake
you will get twenty three!
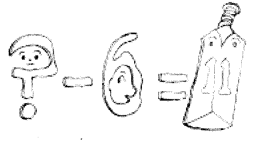
(iii) I am a special number
Take away from me a six!
A whole cricket team
You will still be able to fix!
(iv) Tell me who I am
I shall give you a pretty clue!
you will get me back
If you take me out of twenty two!
Solution:
(i) According to the condition,
I + 12 = 34 or x + 12 = 34
∴ By inspection, we have
22 + 12 = 34
So, I am 22.
(ii) Let I am ‘x’.
We know that there are 7 days in a week.
∴ upcounting from x for 7, the sum = 23
By inspections, we have
16 + 7 = 23
∴ x = 16
Thus I am 16.
(iii) Let the special number be x and there are 11 players in cricket team.
∴ Special Number -6 = 11
∴ x – 6 = 11
By inspection, we get
17 – 6 = 11
∴ x = 17
Thus I am 17.
(iv) Suppose I am ‘x’.
∴ 22 – I = I
or 22 – x = x
By inspection, we have
22 – 11 = 11
∴ x = 11
Thus I am 11.