Practical Geometry Class 6 Extra Questions Maths Chapter 14
Practical Geometry Class 6 Extra Questions Maths Chapter 14
Extra Questions for Class 6 Maths Chapter 14 Practical Geometry
Practical Geometry Class 6 Extra Questions Very Short Answer Type
Question 1.
![]()

Solution:
Step I: Draw a ray OX.
Step II : With centre 0 and radius equal to the length of AB (3.6 cm) mark a point P on the ray.
![]()
Step III: With centre P and radius equal to the length of CD (1.6 cm) mark another point Q on the ray.
Thus OQ is the required segment such that OQ = 3.6 cm + 1.6 cm = 5.2 cm.
Question 2.
Construct a perpendicular to a given line segment at point on it.
Solution:
![]()
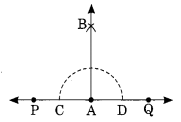
Step II : With centre A draw an arc which meets PQ at C and D.
Step III : Join AB and produce.
Step IV: With centres C and D and radius equal to half of the length of the previous arc, draw two arcs which meets each other at B.
![]()
Question 3.
Construct an angle of 60° and bisect it.
Solution:
![]()
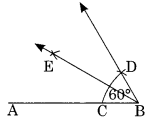
Step II: With centre B and proper radius, draw an arc which meets AB at C.
Step III : With C as centre and the same radius as in step II, draw an arc cutting the previous arc at D.
Step IV : Join B to D and produce.
Step V : Draw the bisector BE of ∠ABD.
Thus BE is the required bisector of ∠ABD.
Question 4.
Draw an angle of 120° and hence construct an angle of 105°.
Solution:
![]()
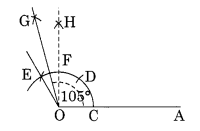
Step II : With centre O and proper radius, draw an arc which meets OA at C.
Step III : With centre C and radius same, mark D and E on the previous arc.
Step IV : Join O to E and produce.
Step V : ∠EOA is the required angle of 120°.
Step VI : Construct an angle of 90° which meets the previous arc at F.
Step VII : With centre E and F and proper radius, draw two arcs which meet each other at G.
Step VIII : Join OG and produce.
Thus ∠GOA is the required angle of 105°.
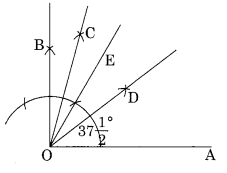
Question 5.
Using compasses and ruler, draw an angle of
![]()
Solution:
Step I: Draw a line segment OA.
Step II : Construct ∠BOA = 90° and ∠EOA = 60°
Step III : Draw OC as the bisector of ∠BOE , which equal to
![]()
Step IV : Draw the bisector OD of ∠COA.
![]()
Question 6.
Draw ∆ABC. Draw perpendiculars from A, B and C respectively on the sides BC, CA and AB. Are there perpendicular concurrent? (passing through the same points).
Solution:
Step I: Draw any ∆ABC.
Step II : Draw the perpendicular AD from A to BC.
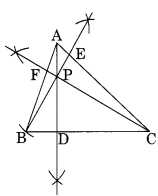
Step III : Draw the perpendicular BE from B to AC.
Step IV : Draw the perpendicular CF from C to AB.
We observe that the perpendiculars AD, BE and CF intersect each other at P.
Thus, P is the point of intersection of the three perpendiculars.
