Linear Equations in One Variable Class 8 Extra Questions Maths Chapter 2
Linear Equations in One Variable Class 8 Extra Questions Maths Chapter 2
Extra Questions for Class 8 Maths Chapter 2 Linear Equations in One Variable
Linear Equations in One Variable Class 8 Extra Questions Very Short Answer Type
Question 1.
Identify the algebraic linear equations from the given expressions.
(a) x2 + x = 2
(b) 3x + 5 = 11
(c) 5 + 7 = 12
(d) x + y2 = 3
Solution:
(a) x2 + x = 2 is not a linear equation.
(b) 3x + 5 = 11 is a linear equation.
(c) 5 + 7 = 12 is not a linear equation as it does not contain variable.
(d) x + y2 = 3 is not a linear equation.
Question 2.
Check whether the linear equation 3x + 5 = 11 is true for x = 2.
Solution:
Given that 3x + 5 = 11
For x = 2, we get
LHS = 3 × 2 + 5 = 6 + 5 = 11
LHS = RHS = 11
Hence, the given equation is true for x = 2
Question 3.
Form a linear equation from the given statement: ‘When 5 is added to twice a number, it gives 11.’
Solution:
As per the given statement we have
2x + 5 = 11 which is the required linear equation.
Question 4.
If x = a, then which of the following is not always true for an integer k. (NCERT Exemplar)

Solution:
Correct answer is (b).
Question 5.
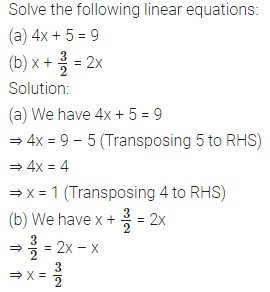
Question 6.


Question 7.
Verify that x = 2 is the solution of the equation 4.4x – 3.8 = 5.
Solution:
We have 4.4x – 3.8 = 5
Putting x = 2, we have
4.4 × 2 – 3.8 = 5
⇒ 8.8 – 3.8 = 5
⇒ 5 = 5
L.H.S. = R.H.S.
Hence verified.
Question 8.

Solution:

⇒ 3x × 3 – (2x + 5) × 4 = 5 × 6
⇒ 9x – 8x – 20 = 30 (Solving the bracket)
⇒ x – 20 = 30
⇒ x = 30 + 20 (Transposing 20 to RHS)
⇒ x = 50
Hence x = 50 is the required solution.
Question 9.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Solution:
Let the angles of a given triangle be 2x°, 3x° and 4x°.
2x + 3x + 4x = 180 (∵ Sum of the angles of a triangle is 180°)
⇒ 9x = 180
⇒ x = 20 (Transposing 9 to RHS)
Angles of the given triangles are
2 × 20 = 40°
3 × 20 = 60°
4 × 20 = 80°
Question 10.
The sum of two numbers is 11 and their difference is 5. Find the numbers.
Solution:
Let one of the two numbers be x.
Other number = 11 – x.
As per the conditions, we have
x – (11 – x) = 5
⇒ x – 11 + x = 5 (Solving the bracket)
⇒ 2x – 11 = 5
⇒ 2x = 5 + 11 (Transposing 11 to RHS)
⇒ 2x = 16
⇒ x = 8
Hence the required numbers are 8 and 11 – 8 = 3.
Question 11.
If the sum of two consecutive numbers is 11, find the numbers.
Solution:
Let the two consecutive numbers be x and x + 1.
As per the conditions, we have
x + x + 1 = 11
⇒ 2x + 1 = 11
⇒ 2x = 11 – 1 (Transposing 1 to RHS)
⇒ 2x = 10
x = 5
Hence, the required numbers are 5 and 5 + 1 = 6.
Linear Equations in One Variable Class 8 Extra Questions Short Answer Type
Question 12.
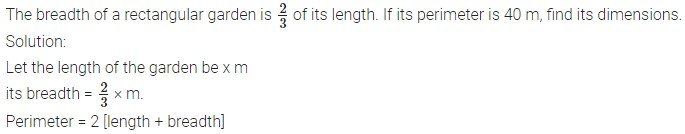

Question 13.
The difference between two positive numbers is 40 and the ratio of these integers is 1 : 3. Find the integers.
Solution:
Let one integer be x.
Other integer = x – 40
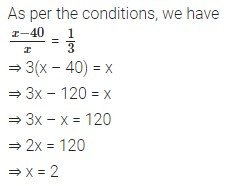
Hence the integers are 60 and 60 – 40 = 20.
Question 14.
Solve for x:

Solution:


Question 15.
The sum of a two-digit number and the number obtained by reversing its digits is 121. Find the number if it’s unit place digit is 5.
Solution:
Unit place digit is given as 5
Let x be the tens place digit
Number formed = 5 + 10x
Number obtained by reversing the digits = 5 × 10 + x = 50 + x
As per the conditions, we have
5 + 10x + 50 + x = 121
⇒ 11x + 55 = 121
⇒ 11x = 121 – 55 (Transposing 55 to RHS)
⇒ 11x = 66
⇒ x = 6
Thus, the tens place digit = 6
Hence the required number = 5 + 6 × 10 = 5 + 60 = 65
Linear Equations in One Variable Class 8 Extra Questions Higher Order Thinking Skills (HOTS)
Question 16.
If the length of the rectangle is increased by 40% and its breadth is decreased by 40%, what will be the percentage change in its perimeter?
Solution:
Let the length of the rectangle be x m and its breadth be y m
Perimeter = 2(x + y)
Now the length of the rectangle becomes after a 40% increase


Question 17.
A fruit seller buys some oranges at the rate of ₹ 5 per orange. He also buys an equal number of bananas at the rate of ₹ 2 per banana. He makes a profit of 20% on oranges and a profit of 15% on bananas. In the end, he sold all the fruits. If he earned a profit of ₹ 390, find the number of oranges.
Solution:
Let the number of oranges bought by him be x and also the number of bananas be x.
Cost of x oranges at the rate of ₹ 5 per orange = ₹ 5x
Cost of x bananas at the rate of ₹ 2 per banana = ₹ 2x

Question 18.
A steamer goes downstream from one point to another in 7 hours. It covers the same distance upstream in 8 hours. If the speed of stream be 2 km/h, find the speed of the steamer in still water and the distance between the ports. (NCERT Exemplar)
Solution:
Let speed of steamer in still water = x km/h
Speed of stream = 2 km/h
Speed downstream = (x + 2) km/h
Speed upstream = (x – 2) km/h
Distance covered in 7 hours while downstream = 7(x + 2)
Distance covered in 8 hours while upstream = 8(x – 2)
According to the condition,
7(x + 2) = 8(x – 2)
⇒ 7x + 14 = 8x – 16
⇒ x = 30 km/h
Total Distance = 7(x + 2) km = 7(30 + 2) km = 7 × 32 km = 224 km.
































