NCERT Solutions For Class 10 Maths Chapter 1 Real Numbers

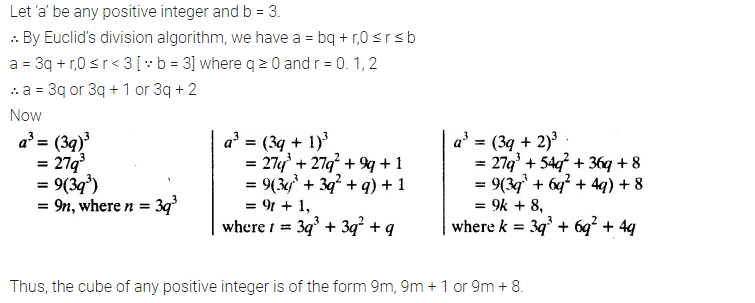
Maths NCERT Solutions For Class 10 Chapter 1 Ex 1.2

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 1 Real Numbers Exercise 1.2

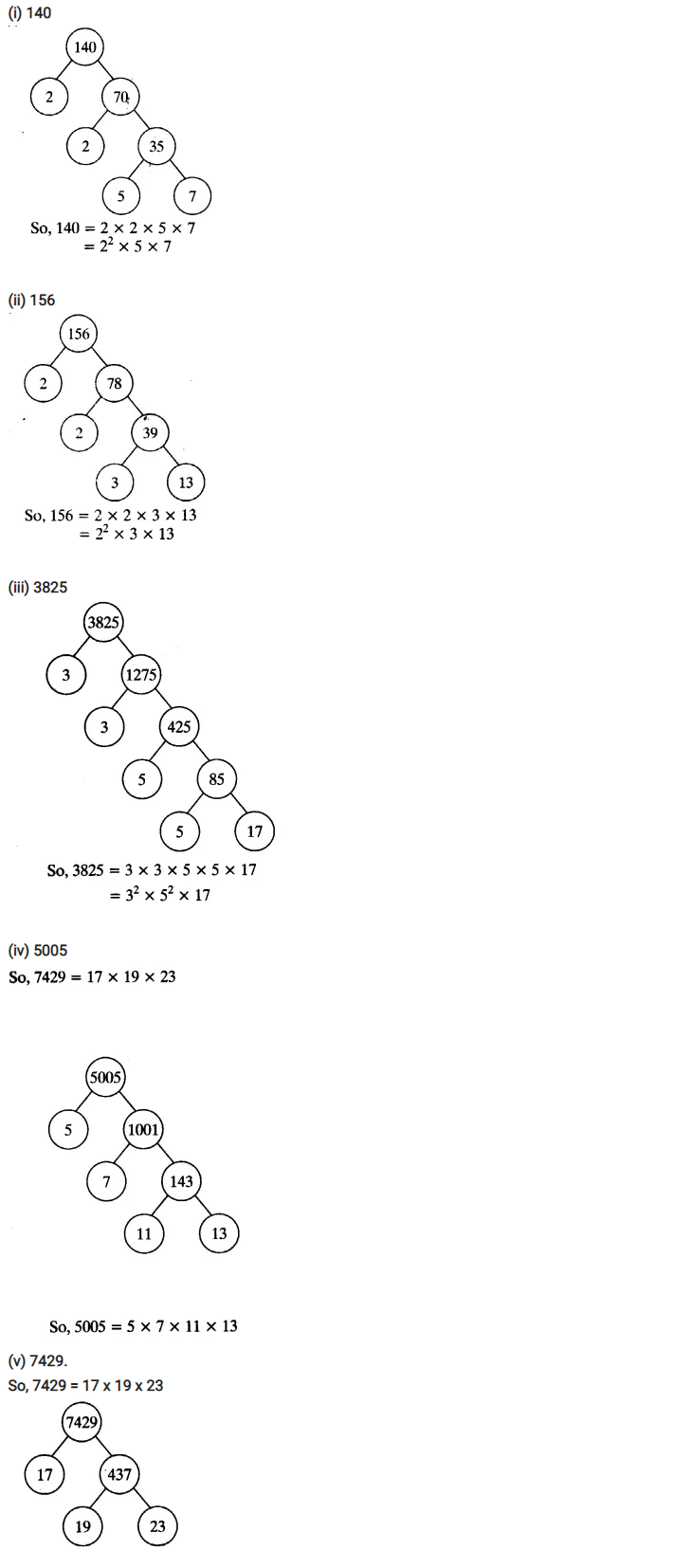
Ex 1.2 Class 10 Maths Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution:

Ex 1.2 Class 10 Maths Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:

Ex 1.2 Class 10 Maths Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:

Ex 1.2 Class 10 Maths Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).

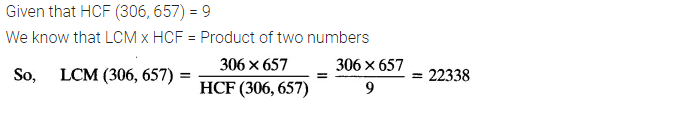
Ex 1.2 Class 10 Maths Question 5.
Check whether 6ⁿ can end with the digit 0 for any natural number n.

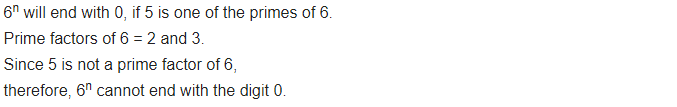
Ex 1.2 Class 10 Maths Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.

Ex 1.2 Class 10 Maths Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 1 Real Numbers Exercise 1.3

Ex 1.3 Class 10 Maths Question 1.
Prove that √5 is irrational.
Solution:

Ex 1.3 Class 10 Maths Question 2.
Show that 3 + √5 is irrational.
Solution:

Ex 1.3 Class 10 Maths Question 3.
Prove that the following are irrational.

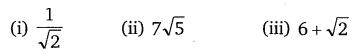
Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 1 Real Numbers Exercise 1.4

Ex 1.4 Class 10 Maths Question 1.
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or non-terminating repeating decimal expansion:

Ex 1.4 Class 10 Maths Question 2.
Write down the decimal expansions of those rational numbers in question 1, which have terminating decimal expansions.

Ex 1.4 Class 10 Maths Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational and of the form pq, what can you say about the prime factors of q?
(i) 43. 123456789
(ii) 0.120120012000120000…
(iii) 43. 123456789¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Real Numbers Class 10 Extra Questions Maths Chapter 1

Extra Questions for Class 10 Maths Chapter 1 Real Numbers. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

You can also download NCERT Solutions For Class 10 Maths to help you to revise the complete syllabus and score more marks in your examinations.

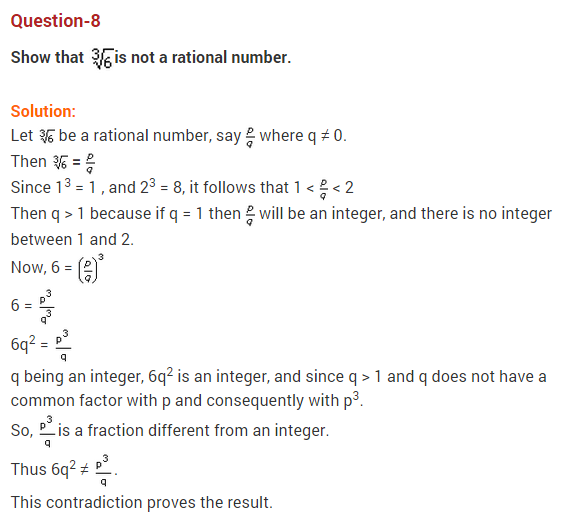
Important Questions for Class 10 Maths Chapter 1 Real Numbers

Real Numbers Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
The decimal expansion of the rational number will terminate after how many places of decimals? (2013)
Solution:

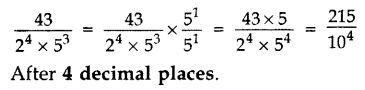
Question 2.
Write the decimal form of
Solution:
Non-terminating non-repeating.

Question 3.
Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11, and 15 respectively.
Solution:
Algorithm
398 – 7 = 391, 436 – 11 = 425, 542 – 15 = 527
HCF of 391, 425, 527 = 17

You can practice more Grade 8 Real Numbers Common Core Questions and Answers to score good marks in the exams.

Question 4.
Express 98 as a product of its primes.
Solution:
2 × 7²

Question 5.
If the HCF of 408 and 1032 is expressible in the form 1032 × 2 + 408 × p, then find the value of p.
Solution:
HCF of 408 and 1032 is 24.
1032 × 2 + 408 × (p) = 24
408p = 24 – 2064
p = -5

Real Numbers Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number. (2012)
Solution:
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 9×459/27 = 153

Question 7.
Find HCF and LCM of 13 and 17 by prime factorisation method. (2013)
Solution:
13 = 1 × 13; 17 = 1 × 17
HCF = 1 and LCM = 13 × 17 = 221

Question 8.
Find LCM of numbers whose prime factorisation are expressible as 3 × 5² and 3² × 7². (2014)
Solution:
LCM (3 × 5², 3² × 7²) = 3² × 5² × 7² = 9 × 25 × 49 = 11025

Question 9.
Find the LCM of 96 and 360 by using fundamental theorem of arithmetic. (2012)
Solution:
96 = 2⁵ × 3
360 = 2³ × 3² × 5
LCM = 2⁵ × 3² × 5 = 32 × 9 × 5 = 1440

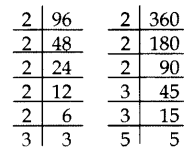
Question 10.
Find the HCF (865, 255) using Euclid’s division lemma. (2013)
Solution:
865 > 255
865 = 255 × 3 + 100
255 = 100 × 2 + 55
100 = 55 × 1 + 45
55 = 45 × 1 + 10
45 = 10 × 4 + 5
10 = 5 × 2 + 0
The remainder is 0.
HCF = 5

Question 11.
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively. (2015)
Solution:
It is given that on dividing 70 by the required number, there is a remainder 5.
This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly, 125 – 8 = 117 is also exactly divisible by the required number.
65 = 5 × 13
117 = 3² × 13
HCF = 13
Required number = 13

Question 12.
Find the prime factorisation of the denominator of rational number expressed as 6.12¯ in simplest form. (2014)
Solution:
Let x = 6.12¯ …(i)
100x = 612.12¯ …(ii)
…[Multiplying both sides by 100]
Subtracting (i) from (ii),
99x = 606
x = 606/99 = 202/33
Denominator = 33
Prime factorisation = 3 × 11

Question 13.
Complete the following factor tree and find the composite number x. (2014)

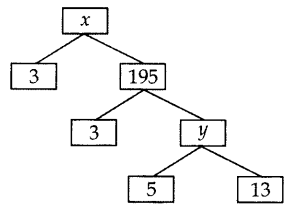
Solution:
y = 5 × 13 = 65
x = 3 × 195 = 585

Question 14.
Prove that 2 + 3√5 is an irrational number. (2014)
Solution:
Let us assume, to the contrary, that 2 + 3√5 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 2 + 3√5 = a/b, where a and b are coprime.
Rearranging the above equation, we get

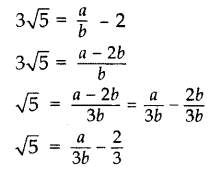
Since a and b are integers, we get a/3b−2/3 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So, we conclude that 2 + 3√5 is irrational.

Question 15.
Show that 3√7 is an irrational number. (2016)
Solution:
Let us assume, to the contrary, that 3√7 is rational.
That is, we can find coprime a and b (b ≠ 0) such that 3√7 = ab
Rearranging, we get √7 = a/3b
Since 3, a and b are integers, a/3b is rational, and so √7 is rational.
But this contradicts the fact that √7 is irrational.
So, we conclude that 3√7 is irrational.

Question 16.
Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number? (2015)
Solution:
17 × 5 × 11 × 3 × 2 + 2 × 11 …(i)
= 2 × 11 × (17 × 5 × 3 + 1)
= 2 × 11 × (255 + 1)
= 2 × 11 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.

Question 17.
Check whether 4n can end with the digit 0 for any natural number n. (2015)
Solution:
4ⁿ = (2²)ⁿ = 2²ⁿ
The only prime in the factorization of 4ⁿ is 2.
There is no other prime in the factorization of 4ⁿ = 2²ⁿ
(By uniqueness of the Fundamental Theorem of Arithmetic).
5 does not occur in the prime factorization of 4ⁿ for any n.
Therefore, 4ⁿ does not end with the digit zero for any natural number n.

Question 18.
Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons. (2017 OD)
Solution:
No, LCM = Product of the highest power of each factor involved in the numbers.
HCF = Product of the smallest power of each common factor.
We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF
We are given that,
LCM = 175 and HCF = 15
175 = k × 15
⇒ 11.67 = k
But in this case, LCM ≠ k × HCF
Therefore, two numbers cannot have LCM as 175 and HCF as 15.

Real Numbers Class 10 Important Questions Short Answer-II (3 Marks)

Question 19.
Prove that √5 is irrational and hence show that 3 + √5 is also irrational. (2012)
Solution:
Let us assume, to the contrary, that √5 is rational.
So, we can find integers p and q (q ≠ 0), such that
√5 = p/q, where p and q are coprime.
Squaring both sides, we get
5 = p2/q2
⇒ 5q² = p² …(i)
⇒ 5 divides p²
5 divides p
So, let p = 5r
Putting the value of p in (i), we get
5q² = (5r)²
⇒ 5q² = 25r²
⇒ q² = 5r²
⇒ 5 divides q²
5 divides q
So, p and q have atleast 5 as a common factor.
But this contradicts the fact that p and q have no common factor.
So, our assumption is wrong, is irrational.
√5 is irrational, 3 is a rational number.
So, we conclude that 3 + √5 is irrational.

Question 20.
Prove that 3 + 2√3 is an irrational number. (2014)
Solution:
Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = a/b, where a and b are coprime.
Rearranging the equations, we get

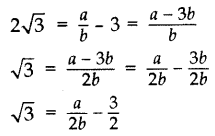
Since a and b are integers, we get a/2b−3/2 is rational and so √3 is rational.
But this contradicts the fact that √3 is irrational.
So we conclude that 3 + 2√3 is irrational.

Question 21.
Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together? (2013)
Solution:
9 = 3², 12 = 2² × 3, 15 = 3 × 5
LCM = 2² × 3² × 5 = 4 × 9 × 5 = 180 minutes or 3 hours
They will next toll together after 3 hours.

Question 22.
Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times. (2012)
Solution:
To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 5² × 17
680 = 2³ × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.

Question 23.
The length, breadth, and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly. (2015)
Solution:
To find the length of the longest rod that can measure the dimensions of the room exactly, we have to find HCF.
L, Length = 8 m 50 cm = 850 cm = 2¹ × 5² × 17
B, Breadth = 6 m 25 cm = 625 cm = 5⁴
H, Height = 4 m 75 cm = 475 cm = 5² × 19
HCF of L, B and H is 5² = 25 cm
Length of the longest rod = 25 cm

Question 24.
Three alarm clocks ring at intervals of 4, 12 and 20 minutes respectively. If they start ringing together, after how much time will they next ring together? (2015)
Solution:
To find the time when the clocks will next ring together,
we have to find LCM of 4, 12 and 20 minutes.
4 = 2²
12 = 2² × 3
20 = 2² × 5

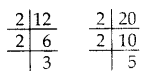
LCM of 4, 12 and 20 = 2² × 3 × 5 = 60 minutes.
So, the clocks will ring together again after 60 minutes or one hour.

Question 25.
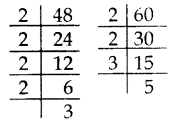
In a school, there are two Sections A and B of class X. There are 48 students in Section A and 60 students in Section B. Determine the least number of books required for the library of the school so that the books can be distributed equally among all students of each Section. (2017 OD)
Solution:
Since the books are to be distributed equally among the students of Section A and Section B. therefore, the number of books must be a multiple of 48 as well as 60.
Hence, required num¬ber of books is the LCM of 48 and 60.
48 = 2⁴ × 3
60 = 2² × 3 × 5
LCM = 2⁴ × 3 × 5 = 16 × 15 = 240
Hence, required number of books is 240.

Question 26.
By using Euclid’s algorithm, find the largest number which divides 650 and 1170. (2017 OD)
Solution:
Given numbers are 650 and 1170.
1170 > 650
1170 = 650 × 1 + 520
650 = 520 × 1 + 130
520 = 130 × 4 + 0
HCF = 130
The required largest number is 130.

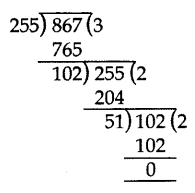
Question 27.
Find the HCF of 255 and 867 by Euclid’s division algorithm. (2014)
Solution:
867 is greater than 255. We apply the division lemma to 867 and 255, to get
867 = 255 × 3 + 102
We continue the process till the remainder is zero
255 = 102 × 2 + 51
102 = 51 × 2 + 0, the remainder is zero.
HCF = 51

Question 28.
Using Euclid’s division algorithm, find whether the pair of numbers 847, 2160 are coprime or not.
To find out the minimum (least) time when the bells toll together next, we find the LCM of 9, 12, 15.
Solution:

Real Numbers Class 10 Important Questions Long Answer (4 Marks)

Question 29.
Prove that 3 + 2√5 is irrational. (2012, 2017 D)
Solution:
Let us assume, to the contrary, that 3 + 2√5 is rational
So that we can find integers a and b (b ≠ 0), such that
3 + 2 √5 = a/b, where a and b are coprime.
Rearranging this equation, we get

Since a and b are integers, we get that a/2b – 3/2 is rational and so √5 is rational.
But this contradicts the fact that √5 is irrational.
So we conclude that 3 + 2√5 is irrational.

Question 30.
There are 104 students in class X and 96 students in class IX in a school. In a house examination, the students are to be evenly seated in parallel rows such that no two adjacent rows are of the same class. (2013)
(a) Find the maximum number of parallel rows of each class for the seating arrange¬ment.
(b) Also, find the number of students of class IX and also of class X in a row.
(c) What is the objective of the school administration behind such an arrangement?
Solution:
104 = 2³ × 13
96 = 2⁵ × 3
HCF = 2³ = 8

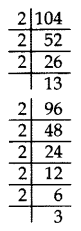
(a) Number of rows of students of class X = 104/8 = 13
Number maximum of rows class IX = 96/8 = 12
Total number of rows = 13 + 12 = 25
(b) No. of students of class IX in a row = 8
No. of students of class X in a row = 8
(c) The objective of school administration behind such an arrangement is fair and clean examination, so that no student can take help from any other student of his/her class.

Question 31.
Dudhnath has two vessels containing 720 ml and 405 ml of milk respectively. Milk from these containers is poured into glasses of equal capacity to their brim. Find the minimum number of glasses that can be filled. (2014)
Solution:
1st vessel = 720 ml; 2nd vessel = 405 ml
We find the HCF of 720 and 405 to find the maximum quantity of milk to be filled in one glass.
405 = 3⁴ × 5
720 = 2⁴ × 3² × 5
HCF = 3² × 5 = 45 ml = Capacity of glass
No. of glasses filled from 1st vessel = 720/45 = 16
No. of glasses filled from 2nd vessel = 405/45 = 9
Total number of glasses = 25

Question 32.
Amita, Sneha, and Raghav start preparing cards for all persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together? (2013)
Solution:
To find the earliest (least) time, they will start preparing a new card together, we find the LCM of 10, 16 and 20.
10 = 2 × 5
16 = 2⁴
20 = 2² × 5
LCM = 2⁴ × 5 = 16 × 5 = 80 minutes
They will start preparing a new card together after 80 minutes.

Question 33.
Find HCF of numbers 134791, 6341 and 6339 by Euclid’s division algorithm. (2015)
Solution:
First, we find HCF of 6339 and 6341 by Euclid’s division method.

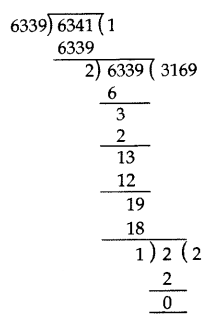
6341 > 6339
6341 = 6339 × 1 + 2
6339 = 2 × 3169 + 1
2 = 1 × 2 + 0
HCF of 6341 and 6339 is 1.
Now, we find the HCF of 134791 and 1
134791 = 1 × 134791 + 0
HCF of 134791 and 1 is 1.
Hence, the HCF of the given three numbers is 1.

Question 34.
If two positive integers x and y are expressible in terms of primes as x = p²q³ and y = p³q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain. (2014)
Solution:
x = p²q³ and y = p³q
LCM = p³q³
HCF = p²q …..(i)
Now, LCM = p³q³
⇒ LCM = pq² (p²q)
⇒ LCM = pq² (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 2² × 3
b = 18 = 2 × 3²
HCF = 2 × 3 = 6 …(ii)
LCM = 2² × 3² = 36
LCM = 6 × 6
LCM = 6 (HCF) …[From (ii)]
Here LCM is 6 times HCF.

Question 35.
Show that one and only one out of n, (n + 1) and (n + 2) is divisible by 3, where n is any positive integer. (2015)
Solution:
Let n, n + 1, n + 2 be three consecutive positive integers.
We know that n is of the form 3q, 3q + 1, or 3q + 2.
Case I. When n = 3q,
In this case, n is divisible by 3,
but n + 1 and n + 2 are not divisible by 3.
Case II. When n = 3q + 1,
In this case n + 2 = (3q + 1) + 2
= 3q + 3
= 3(q + 1 ), (n + 2) is divisible by 3,
but n and n + 1 are not divisible by 3.
Case III.
When n = 3q + 2, in this case,
n + 1 = (3q + 2) + 1
= 3q + 3 = 3 (q + 1 ), (n + 1) is divisible by 3,
but n and n + 2 are not divisible by 3.
Hence, one and only one out of n, n + 1 and n + 2 is divisible by 3.

Question 36.
Find the HCF and LCM of 306 and 657 and verify that LCM × HCF = Product of the two numbers. (2016 D)
Solution:
306 = 2 × 3² × 17
657 = 32 × 73
HCF = 3² = 9
LCM = 2 × 3² × 17 × 73 = 22338
L.H.S. = LCM × HCF = 22338 × 9 = 201042
R.H.S. = Product of two numbers = 306 × 657 = 201042
L.H.S. = R.H.S.

Question 37.
Show that any positive odd integer is of the form 41 + 1 or 4q + 3 where q is a positive integer. (2016 OD)
Solution:
Let a be a positive odd integer
By Euclid’s Division algorithm:
a = 4q + r …[where q, r are positive integers and 0 ≤ r < 4]
a = 4q
or 4q + 1
or 4q + 2
or 4q + 3
But 4q and 4q + 2 are both even
a is of the form 4q + 1 or 4q + 3.

CBSE Class 10 Maths Notes Chapter 1 Real Numbers

R = Real Numbers:
All rational and irrational numbers are called real numbers.

I = Integers:
All numbers from (…-3, -2, -1, 0, 1, 2, 3…) are called integers.

Q = Rational Numbers:
Real numbers of the form p/q, q ≠ 0, p, q ∈ I are rational numbers.

• All integers can be expressed as rational, for example, 5 = 51
• Decimal expansion of rational numbers terminating or non-terminating recurring.

Q’ = Irrational Numbers:
Real numbers which cannot be expressed in the form p/q and whose decimal expansions are non-terminating and non-recurring.

• Roots of primes like √2, √3, √5 etc. are irrational

N = Natural Numbers:
Counting numbers are called natural numbers. N = {1, 2, 3, …}

W = Whole Numbers:
Zero along with all natural numbers are together called whole numbers. {0, 1, 2, 3,…}

Even Numbers:
Natural numbers of the form 2n are called even numbers. (2, 4, 6, …}

Odd Numbers:
Natural numbers of the form 2n -1 are called odd numbers. {1, 3, 5, …}

• Why can’t we write the form as 2n+1?

Remember this!

• All Natural Numbers are whole numbers.
• All Whole Numbers are Integers.
• All Integers are Rational Numbers.
• All Rational Numbers are Real Numbers.

Prime Numbers:
The natural numbers greater than 1 which are divisible by 1 and the number itself are called prime numbers, Prime numbers have two factors i.e., 1 and the number itself For example, 2, 3, 5, 7 & 11 etc.

• 1 is not a prime number as it has only one factor.

Composite Numbers:
The natural numbers which are divisible by 1, itself and any other number or numbers are called composite numbers. For example, 4, 6, 8, 9, 10 etc.
Note: 1 is neither prime nor a composite number.

I. Euclid’s Division lemma
Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r ≤ b.
Notice this. Each time ‘r’ is less than b. Each ‘q’ and ‘r’ is unique.

II. Application of lemma
Euclid’s Division lemma is used to find HCF of two positive integers. Example: Find HCF of 56 and 72 ?
Steps:

• Apply lemma to 56 and 72.
• Take bigger number and locate ‘b’ and ‘r’. 72 = 56 × 1 + 16
• Since 16 ≠ 0, consider 56 as the new dividend and 16 as the new divisor. 56 = 16 × 3 + 8
• Again, 8 ≠ 0, consider 16 as new dividend and 8 as new divisor. 16 = 8 × 2 + 0

Since remainder is zero, divisor (8) is HCF.
Although Euclid’s Division lemma is stated for only positive integers, it can be extended for all integers except zero, i.e., b ≠ 0.

III. Constructing a factor tree
Steps

• Write the number as a product of prime number and a composite number
  Example:
  Factorize 48
• Repeat the process till all the primes are obtained
  ∴ Prime factorization of 48 = 2⁴ x 3
  

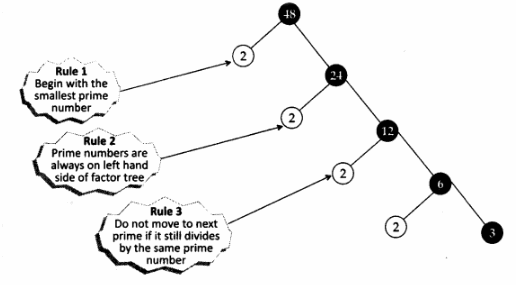
IV. Fundamental theorem of Arithmetic
Every composite number can be expressed as a product of primes, and this expression is unique, apart from the order in which they appear.
Applications:

1. To locate HCF and LCM of two or more positive integers.
2. To prove irrationality of numbers.
3. To determine the nature of the decimal expansion of rational numbers.

1. Algorithm to locate HCF and LCM of two or more positive integers:

Step I:
Factorize each of the given positive integers and express them as a product of powers of primes in ascending order of magnitude of primes.
Step II:
To find HCF, identify common prime factor and find the least powers and multiply them to get HCF.
Step III:
To find LCM, find the greatest exponent and then multiply them to get the LCM.

2. To prove Irrationality of numbers:

• The sum or difference of a rational and an irrational number is irrational.
• The product or quotient of a non-zero rational number and an irrational number is irrational.

3. To determine the nature of the decimal expansion of rational numbers:

• Let x = p/q, p and q are co-primes, be a rational number whose decimal expansion terminates. Then the prime factorization of’q’ is of the form 2^m5ⁿ, m and n are non-negative integers.
• Let x = p/q be a rational number such that the prime factorization of ‘q’ is not of the form 2^m5ⁿ, ‘m’ and ‘n’ being non-negative integers, then x has a non-terminating repeating decimal expansion.

Alert!

• 2³ can be written as: 2³ = 2³5⁰
• 5² can be written as: 5² = 2⁰5²

SabDekho

The Complete Educational Website

Bihar Board

UP Board

IAS Notes

Jac Board

MP Board

सम्पूर्ण व्याकरण

जीवनी

निबंध

टेन्स

सामान्य ज्ञान

Rajasthan Board