NCERT Solutions for Class 10 Maths Chapter 11 Constructions
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1
Ex 11.1 Class 10 Maths Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
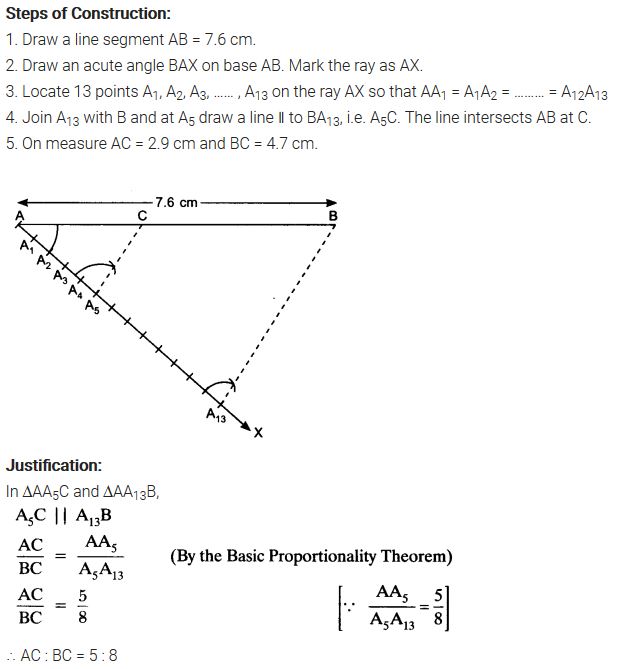
Ex 11.1 Class 10 Maths Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Solution:
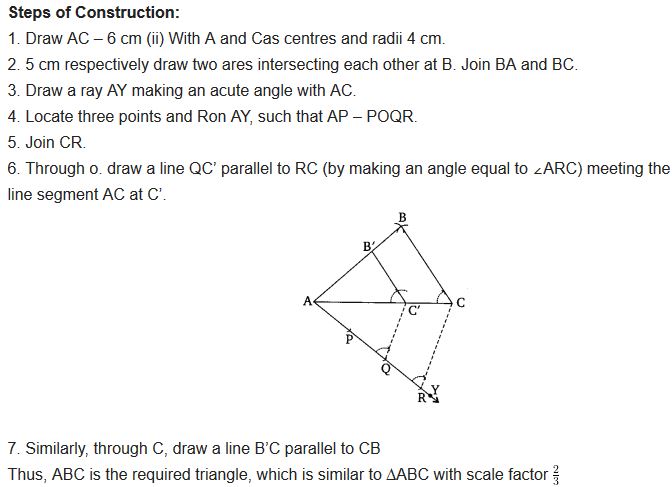

You can also download the free PDF of Ex 11.1 Class 10 Constructions NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Ex 11.1 Class 10 Maths Question 3.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Solution:
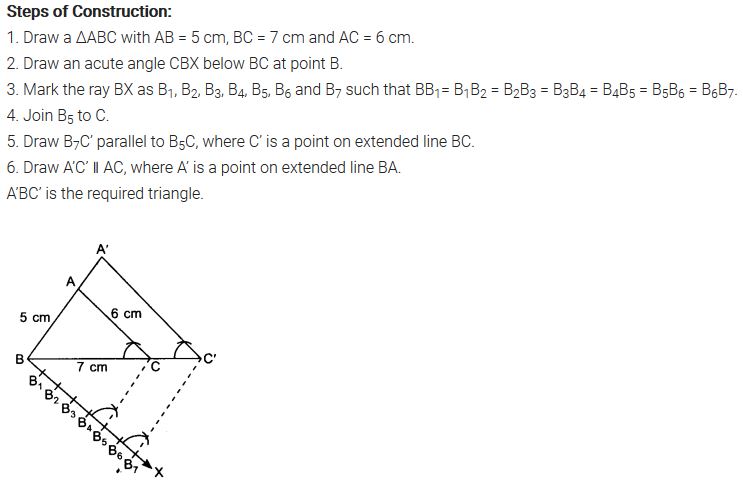

Ex 11.1 Class 10 Maths Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1 1/2 times the corresponding sides of the isosceles triangle.
Solution:
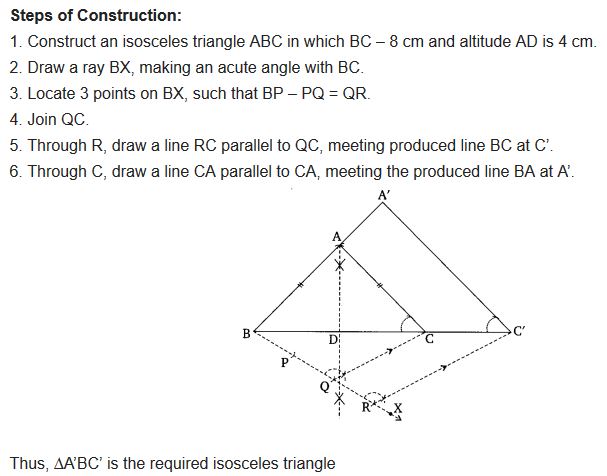

Ex 11.1 Class 10 Maths Question 5.
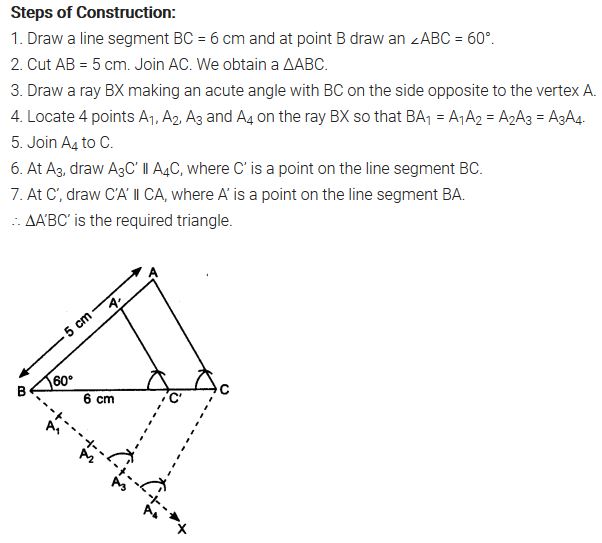
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Solution:

Ex 11.1 Class 10 Maths Question 6.
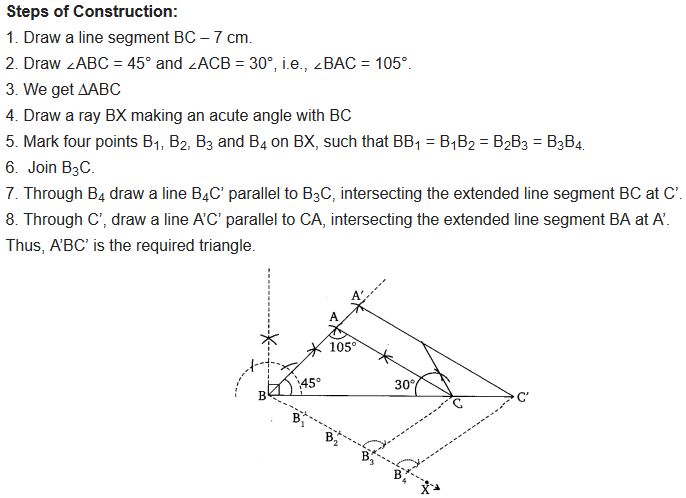
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ABC.
Solution:

Ex 11.1 Class 10 Maths Question 7.
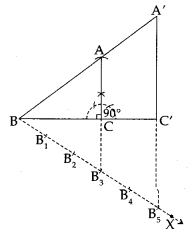
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3F times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. Construct a ∆ABC, such that BC = 4 cm, CA = 3 cm and ∠BCA = 90°
2. Draw a ray BX making an acute angle with BC.
3. Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
4. Join B3C.
5. Through B5, draw B5C’ parallel to B3C intersecting BC produced at C’.
6. Through C’, draw C’A’ parallel to CA intersecting AB produced at A’.
Thus, ∆A’BC’ is the required right triangle.
Justification:

Class 10 Maths Constructions Mind Maps
Construction
Construction implies drawing geometrical figures accurately such that triangles, quadrilateral and circles with the help of ruler and compass.
Division of a Line Segment
A line segment can be divided in a given ratio (both internally and externally)
Example:
Divide a line segment of length 12 cm internally in the ratio 3:2.
Solution :
Steps of construction :
(i) Draw a line segment AB = 12 cm. by using a ruler.
(ii) Draw a ray making a suitable acute angle ∠BAX with AB.
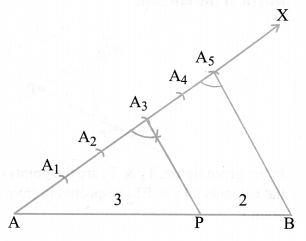
(iii) Along AX, draw 5 ( = 3 + 2) arcs intersecting the ray AX at A1? A2, A3, A4 and A5 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5
(iv) Join BA5.
(v) Through A3 draw a line A3P parallel to A5B making ∠AA3P = ∠AA5B, intersecting AB at point P.
The point P so obtained is the required point, which divides AB internally in the ratio 3 : 2.
Similar Triangles
(i) This Construction involves two different situation.
(a) Construction of a similar triangle smaller than the given triangle.
(b) Construction of a similar triangle greater than the given triangle.
(ii) The ratio of sides of the triangle to be constructed with the corresponding sides of the given triangle is called scale factor.
Example:
Draw a triangle ABC with side BC = 7 cm. ∠B = 45°, ∠A = 105°. Construct a triangle whose sides are (4/3) times the corresponding side of ∆ABC.
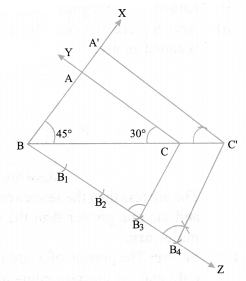
Solution :
Steps of construction :
(i) Draw BC = 7 cm.
(ii) Draw a ray BX and CY such that ∠CBX= 45° and
∠BCY = 180° – (45° + 105°) = 30°
Suppose BX and CY intersect each other at A.
∆ABC so obtained is the given triangle.
(iii) Draw a ray BZ making a suitable acute angle with BC on opposite side of vertex A with respect to BC.
(iv) Draw four (greater of 4 and 3 in 4/3) arcs intersecting the ray BZ at B1, B2, B3, B4 such that BB1 = B1B2 = B2B3 = B3B4.
(v) Join B3 to C and draw a line through B4 parallel to B3C, intersecting the extended line segment BC at C’.
(vi) Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’. Triangle A’BC’ so obtained is the required triangle.
Tangents to a Circle
Two tangents can be drawn to a given circle from a point outside it.
Example:
Draw a circle of radius 4 cm. Take a point P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
Solution :
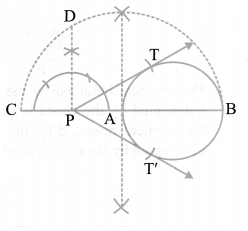
Steps of construction :
(i) Draw a circle of radius 4 cm.
(ii) Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
(iii) Produce AP to C such that AP = CP.
(iv) Draw a semi-circle with CB as diameter.
(v) Draw PD ⊥ CB, intersecting the semi-circle at D.
(vi) With P as centre and PD as radius draw arcs to intersect the given circle at T and T’
(vii) Join PT and PT’. Then, PT and PT’ are the required tangents.
Note:
If centre of a circle is not given, then it can be located by finding point of intersection of perpendicular bisector, of any two nonparallel chords of a circle.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2
Ex 11.2 Class 10 Maths Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:

Ex 11.2 Class 10 Maths Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:

Ex 11.2 Class 10 Maths Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
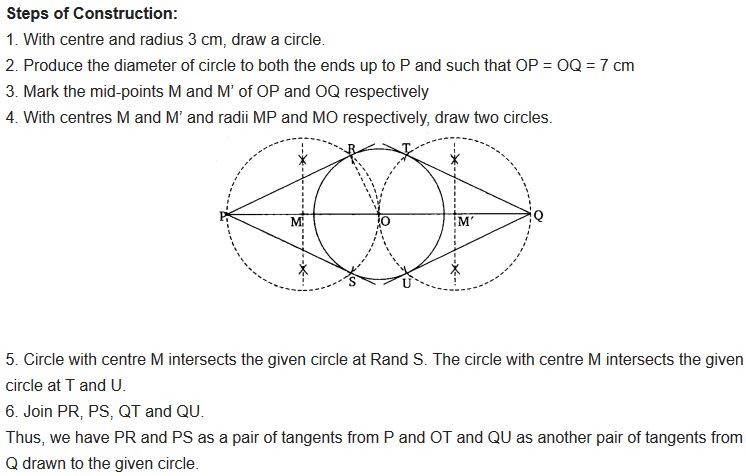

Ex 11.2 Class 10 Maths Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:
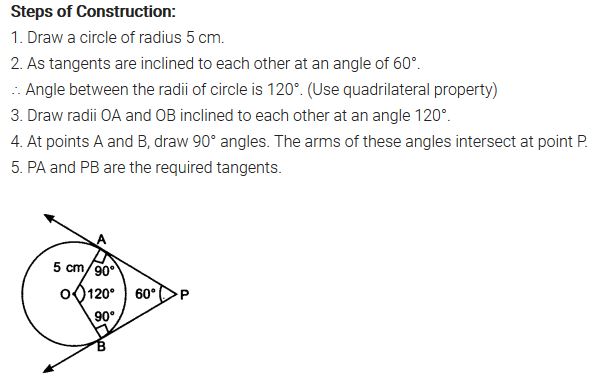

Ex 11.2 Class 10 Maths Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
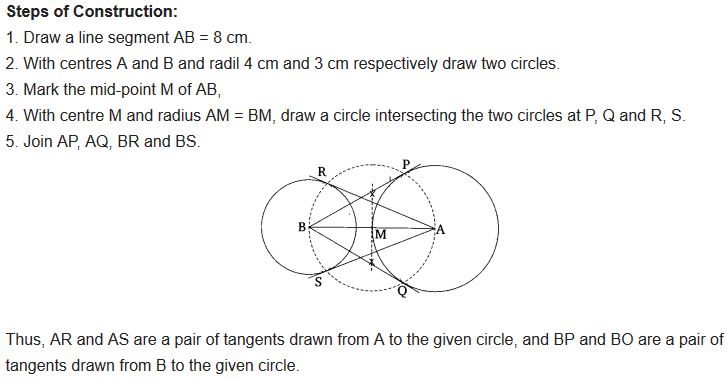
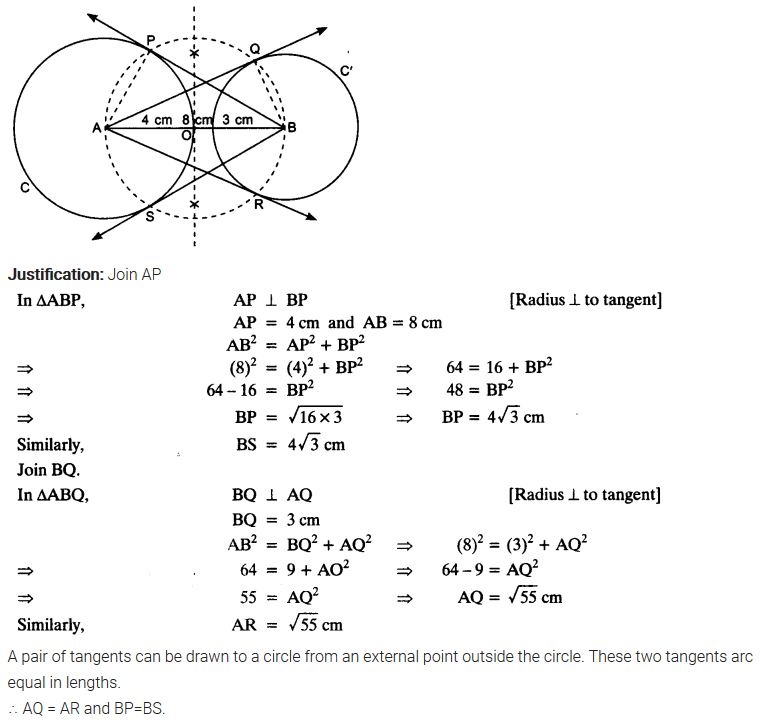
Ex 11.2 Class 10 Maths Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
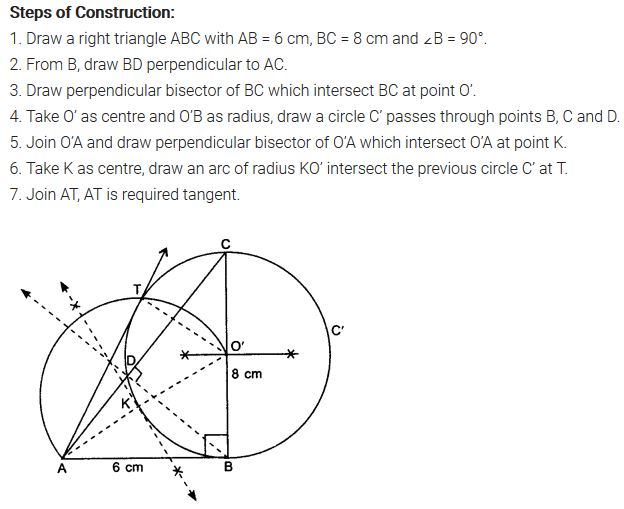

Ex 11.2 Class 10 Maths Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
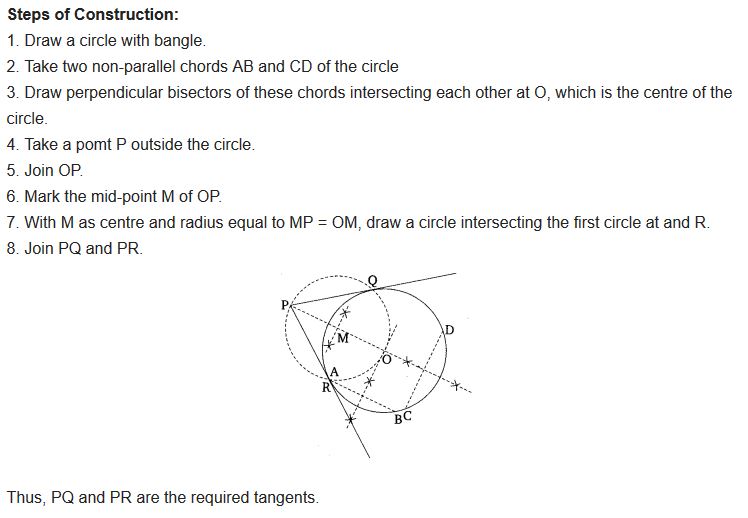
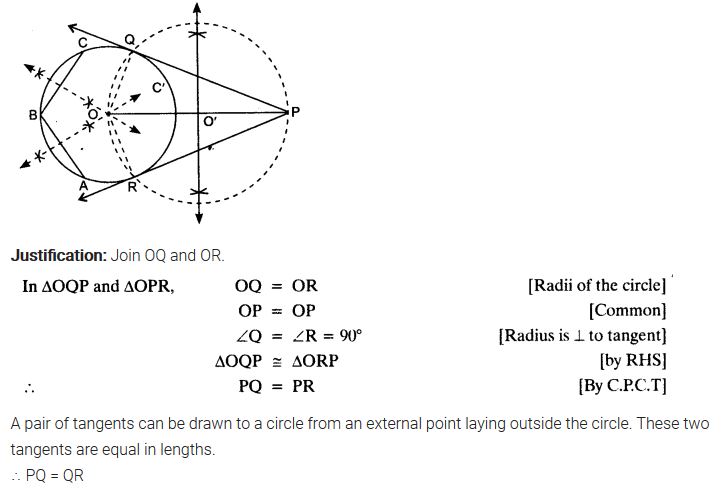
Constructions Class 10 Extra Questions Maths Chapter 11








Important Questions for Class 10 Maths Chapter 11 Constructions
Constructions Class 10 Important Questions Short Answer-I (2 Marks)
Question 1.
Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it which divides it in the ratio 3 : 4. (2011D)
Solution:
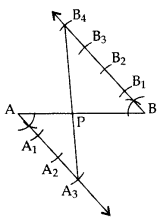
Hence, PA : PB = 3 : 4
Question 2.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that AP/AB=3/5. (2011OD)
Solution:
AB = 7 cm, AB = AP/AB=3/5 … [Given
∴ AP : PB = 3 : 2
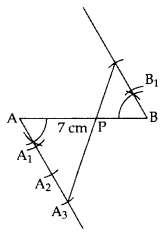
Hence, AP : AB = 3 : 5 or AP/AB=3/5
Constructions Class 10 Important Questions Short Answer-II (3 Marks)
Question 3.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Then construct a triangle whose sides are 5/7 times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC
AB = 5 cm
BC = 6 cm
∠ABC = 60°
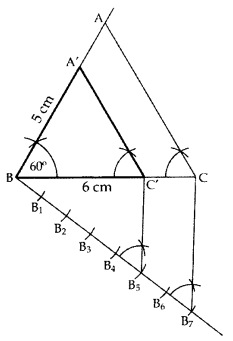
Hence, ∆A’BC’ is the required ∆.
Question 4.
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are 3/5 times the corresponding sides of the given triangle. (20140D)
Solution:
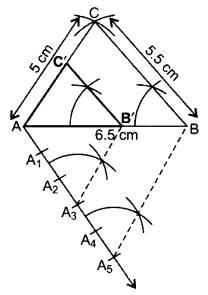
∴ ∆AB’C’ is the required ∆.
Question 5.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are 3/5 times the corresponding sides of the given triangle. (2012D)
Solution:
Here AB = 8 cm, BC = 6 cm and
Ratio = 3/5 of corresponding sides
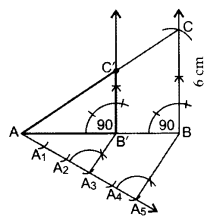
∴ ∆AB’C’ is the required triangle.
Question 6.
Draw a triangle PQR such that PQ = 5 cm, ∠P = 120° and PR = 6 cm. Construct another triangle whose sides are 3/4 times the corresponding sides of ∆PQR. (2011D)
Solution:
In ∆PQR,
PQ = 5 cm, PR = 6 cm, ∠P = 120°
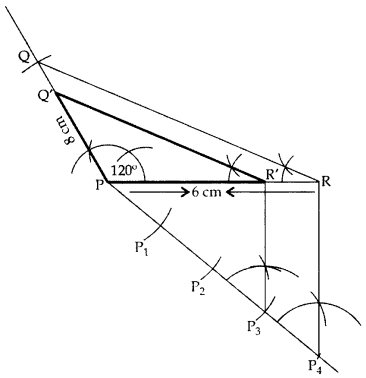
∴ ∆POʻR’ is the required ∆.
Question 7.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle, whose sides are 3/5 times the corresponding sides of ∆ABC. (2012OD)
Solution:
Here, BC = 7 cm, ∠B = 45°, ∠C = 60° and ratio is 3/5 times of corresponding sides
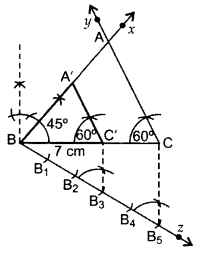
∴ ∆A’BC’ is the required triangle.
Question 8.
Construct a triangle with sides 5 cm, 4 cm and 6 cm. Then construct another triangle whose sides are 2/3 times the corresponding sides of first triangle. (2013D)
Solution:
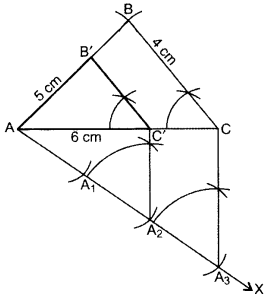
Steps of Construction:
- Draw ∆ABC with AC = 6 cm, AB = 5 cm, BC = 4 cm.
- Draw ray AX making an acute angle with AÇ.
- Locate 3 equal points A1, A2, A3 on AX.
- Join CA3.
- Join A2C’ || CA3.
- From point C’ draw B’C’ || BC.
∴ ∆AB’C’ is the required triangle.
Question 9.
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°. (2011OD)
Solution:
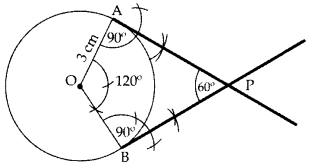
∴ PA & PB are the required tangents.
Question 10.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. (2013D)
Solution:
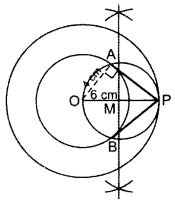
Steps of Construction:
Draw two circles with radius OA = 4 cm and OP = 6 cm with O as centre. Draw ⊥ bisector of OP at M. Taking M as centre and OM as radius draw another circle intersecting the smaller circle at A and B and touching the bigger circle at P. Join PA and PB. PA and PB are the required tangents.
Verification:
In rt. ∆OAP,
OA2 + AP2 = OP2 … [Pythagoras’ theorem
(4)2 + (AP)2 = (6)2
AP2 = 36 – 16 = 20
AP = + √20=√4×5
= 2√5 = 2(2.236) = 4.472 = 4.5 cm
By measurement, ∴ PA = PB = 4.5 cm
Question 11.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°. (2013OD)
Solution:
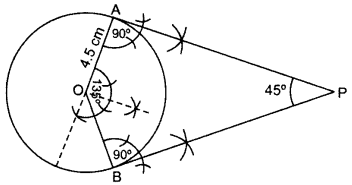
Draw ∠AOB = 135°, ∠OAP = 90°, ∠OBP = 90°
∴ PA and PB are the required tangents.
Question 12.
Draw two tangents to a circle of radius 3.5 cm, from a point P at a distance of 6.2 cm from its cehtre. (2013OD)
Solution:
OP = OC + CP = 3.5 + 2.7 = 6.2 cm
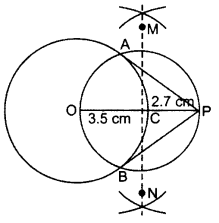
Hence AP & PB are the required tangents.
Question 13.
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle. (2014D, 2015OD)
Solution:
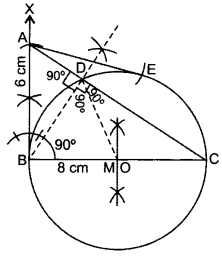
Steps of Construction:
- Draw BC = 8 cm.
- From B draw an angle of 90°.
- Draw an arc BA = 6 cm cutting the angle at A.
- Join AC. ∴ ∆ABC is the required ∆.
- Draw ⊥ bisector of BC cutting BC at M.
- Take Mas centre and BM as radius, draw a circle.
- Take A as centre and AB as radius draw an arc cutting the circle at E. Join AE.
AB and AE are the required tangents.
Justification: ∠ABC = 90° …[Given
Since, OB is a radius of the circle.
∴ AB is a tangent to the circle.
Also, AE is a tangent to the circle.
Question 14.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. (2014OD)
Solution:
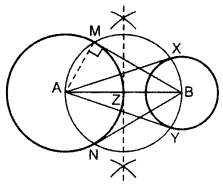
Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the reqd. tangents from external point B.
AX, AY are the reqd. tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴ BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
Constructions Class 10 Important Questions Long Answer (4 Marks).
Question 15.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45° and ∆A = 105°. Then construct a triangle whose sides are 3/5times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [angle sum property of a ∆
105° + 45° + C = 180°
∠C = 180° – 105° – 45o = 30°
BC = 7 cm
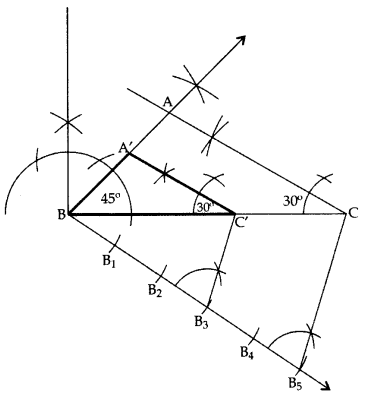
∴ ∆A’BC’ is the required ∆.
Question 16.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are 2/3 times the corresponding sides of ∆ABC. (2012D)
Solution:
Here, BC = 6 cm, ∠A = 105o and ∠C = 30°
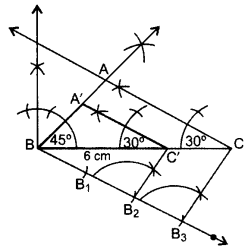
In ∆ABC,
∠A + ∠B + ∠C = 180° …[Angle-sum-property of a ∆
105° + ∠B + 30o = 180°
∠B = 180° – 105° – 30o = 45°
∴ ∆A’BC’ is the required ∆.
Question 17.
Draw a triangle with sides 5 cm, 6 cm and 7 cm. Then construct another triangle whose sides are 2/3 times the corresponding sides of the first triangle. (2012OD)
Solution:
Here, AB = 5 cm, BC = 7 cm, AC = 6 cm and ratio is 2/3 times of corresponding sides.
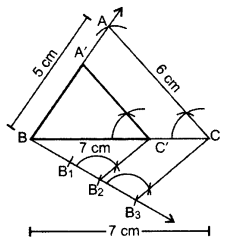
∴ ∆A’BC’ is the required triangle.
Question 18.
Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the isosceles triangle. (2015D)
Solution:
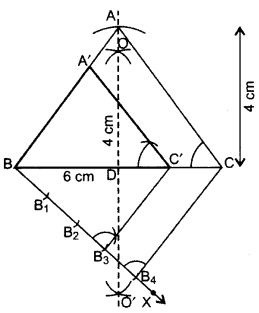
∴ ∆A’BC’ is the required triangle.
Question 19.
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle. (2015D)
Solution:
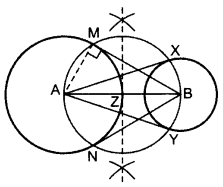
Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the required tangents from external point B.
AX, AY are the required tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
Question 20.
Construct a ∆ABC in which AB = 6 cm, ∠A = 30° and ∆B = 60°. Construct another ∆AB’C’ similar to ∆ABC with base AB’ = 8 cm. (2015OD)
Solution:
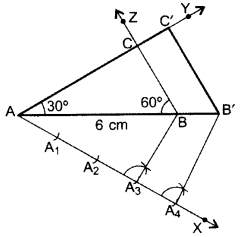
Steps of construction:
- Draw a ∆ABC with side AB = 6 cm, ∠A = 30° and ∠B = 60°.
- Draw a ray AX making an acute angle with AB on the opposite side of point C.
- Locate points A1, A2, A3 and A4 on AX.
- Join A3B. Draw a line through A4 parallel to A3B intersecting extended AB at B’.
- Draw a line parallel to BC intersecting ray AY at C’.
Hence, ∆AB’C’ is the required triangle.
Question 21.
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Now construct another triangle whose sides are 5/7 times the corresponding sides of ∆ABC. (2015OD)
Solution:
In ∆ABC, AB = 5 cm; BC = 6 cm; ∠ABC = 60°
∴ ∆A’BC’ is the required ∆.
Question 22.
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are 3/4 times the corresponding sides of ∆ABC. (2016D)
Solution:
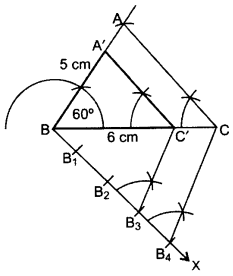
Steps of Construction:
- Draw ∆ABC with the given data.
- Draw a ray BX downwards making an acute angle with BC.
- Locate 4 points B1, B2, B3, B4, on BX, such that BB1 = B1B2 = B2B3 = B3B4.
- Join CB4.
- From B3 draw a line C’B3 || CB4 intersecting BC at C’.
- From C’ draw A’C’ || AC intersecting AB at B’.
Then ∆AB’C’ in the required triangle.
Justification:

Question 23.
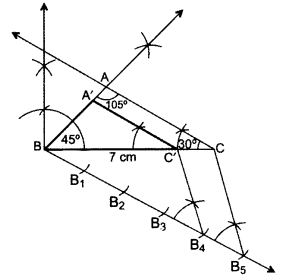
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are 4/5 times the corresponding sides of ∆ABC. (2016D)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° ..[Angle-sum-property of a ∆
105° + 45° + ∠C = 180°
∠C = 180° – 105° – 45o = 30°
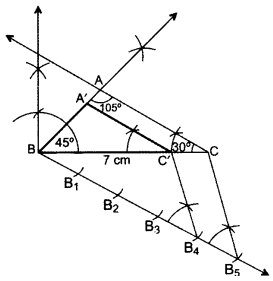
∴ A’BC’ is the required triangle.
Question 24.
Draw an isosceles ∆ABC in which BC = 5.5 cm and altitude AL = 3 cm. Then construct another triangle whose sides are 3/4 of the corresponding sides of ∆ABC. (2016OD)
Solution:
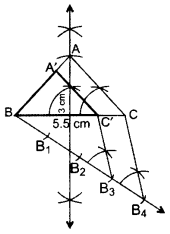
∴ ∆ABC’ is the required ∆.
Question 25.
Draw a triangle with sides 5 cm, 6 cm and 7 cm. Then draw another triangle whose sides are 4/5 of the corresponding sides of first triangle. (2016OD)
Solution:
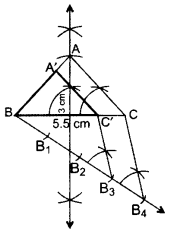
∴ ∆A’BC’ is the required ∆.
Question 26.
Draw two concentric cirlces of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length. (2016D)
Solution:
We have, OD = 3 cm and OP = 5 cm
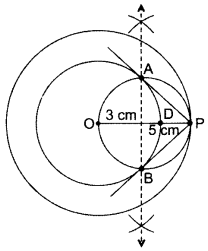
PA and PB are the required tangents
By measurement PA = PB = 4 cm.
Question 27.
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other. (2013, 2016OD)
Solution:
Draw a circle with O as centre and radius 4 cm.
Draw any ∠AOB = 120°. From A and B draw ∠PAO = ∠PBO = 90° which meet at P.
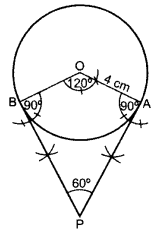
∴ PA and PB are the required tangents.
CBSE Class 10 Maths Notes Chapter 11 Constructions
Determining a Point Dividing a given Line Segment, Internally in the given Ratio M : N
Let AB be the given line segment of length x cm. We are required to determine a point P dividing it internally in the ratio m : n.
Steps of Construction:
- Draw a line segment AB = x cm.
- Make an acute ∠BAX at the end A of AB.
- Use a compass of any radius and mark off arcs. Take (m + n) points A1, A2, … Am, Am+1, …, Am+n along AX such that AA1 = A1A2 = … = Am+n-1 , Am+n
- Join Am+nB.
- Passing through Am, draw a line AmP || Am+nB to intersect AB at P. The point P so obtained is the A required point which divides AB internally in the ratio m : n.

Construction of a Tangent at a Point on a Circle to the Circle when its Centre is Known
Steps of Construction:
- Draw a circle with centre O of the given radius.

- Take a given point P on the circle.
- Join OP.

- Construct ∠OPT = 90°.

- Produce TP to T’ to get TPT’ as the required tangent.

Construction of a Tangent at a Point on a Circle to the Circle when its Centre is not Known
If the centre of the circle is not known, then we first find the centre of the circle by drawing two non-parallel chords of the circle. The point of intersection of perpendicular bisectors of these chords gives the centre of the circle. Then we can proceed as above.
Construction of a Tangents from an External Point to a Circle when its Centre is Known
Steps of Construction:
- Draw a circle with centre O.
- Join the centre O to the given external point P.
- Draw a right bisector of OP to intersect OP at Q.
- Taking Q as the centre and OQ = PQ as radius, draw a circle to intersect the given circle at T and T’.
- Join PT and PT’ to get the required tangents as PT and PT’.

Construction of a Tangents from an External Point to a Circle when its Centre is not Known
If the centre of the circle is not known, then we first find the centre of the circle by drawing two non-parallel chords of a circle. The point of intersection of perpendicular bisectors of the chords gives the centre of the circle. Then we can proceed as above.
Construction of a Triangle Similar to a given Triangle as per given Scale Factor m/n , m < n.
Let ΔABC be the given triangle. To construct a ΔA’B’C’ such that each of its sides is m/n (m < n) of the corresponding sides of ΔABC.
Steps of Construction:
- Construct a triangle ABC by using the given data.
- Make an acute angle ∠BAX, below the base AB.
- Along AX, mark n points A1, A2 …, An, such that AA1 = A1A2 = … = Am-1 Am = … An-1 An.
- Join AnB.
- From Am, draw AmB’ parallel to AnB, meeting AB at B’.
- From B’, draw B’C’ parallel to BC, meeting AC at C’.
Triangle AB’C’ is the required triangle, each of whose sides is m/n (m < n) of the corresponding sides of ΔABC.

Construction of a Triangle Similar to a given Triangle as per given Scale Factor mn , m > n.
Let ΔABC be the given triangle and we want to construct a ΔAB’C’, such that each of its sides is mn (m > n) of the corresponding side of ΔABC.
Steps of Construction:
- Construct a ΔABC by using the given data.
- Make an acute angle ∠BAX, below the base AB. Extend AB to AY and AC to AZ.
- Along AX, mark m points A1, A2 …, An, ..Am, such that AA1 = A1A2 = A2A3 = … = An-1 An = … = Am-1 Am
- Join AnB.
- From Am, draw AmB’ parallel to AnB, meeting AY produced at B’.
- From B’, draw B’C’ parallel to BC, meeting AZ produced at C’.
- Triangle AB’C’ is the required triangle, each of whose sides is (m/n) (m > n) of the corresponding sides of ΔABC.

