NCERT Solutions For Class 10 Maths Chapter 14 Statistics

NCERT Solutions For Class 10 Maths Chapter 14 Statistics

NCERT Solutions For Class 10 Maths Chapter 14 Statistics Ex 14.1

Ex 14.1 Class 10 Maths Question 1.
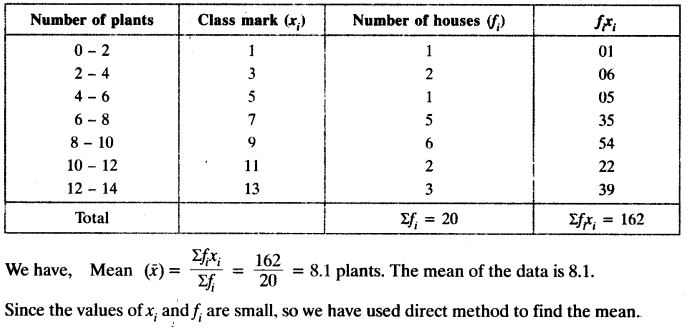
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

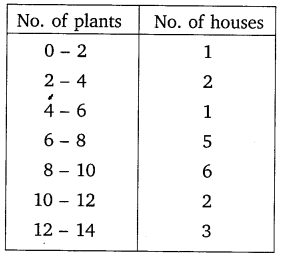
Which method did you use for finding the mean, and why?
Solution:

You can also download the free PDF of  Ex 14.1 Class 10 Statistics NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

 

Ex 14.1 Class 10 Maths Question 2.
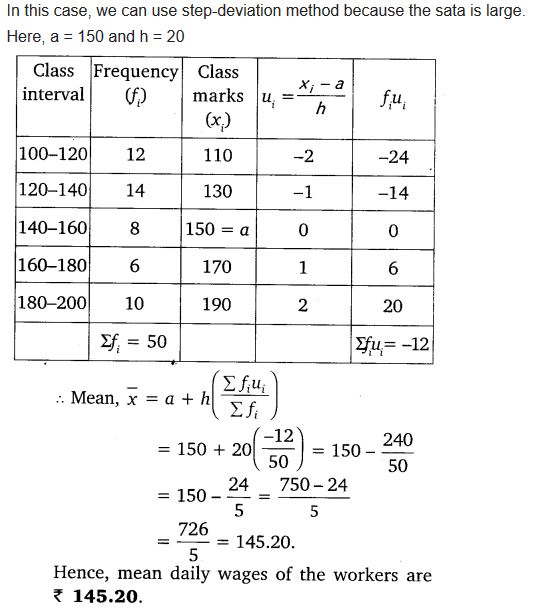
Consider the following distribution of daily wages of 50 workers of a factory.

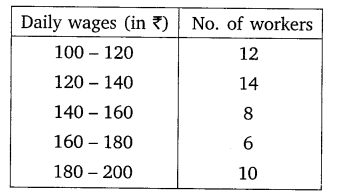
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:

Ex 14.1 Class 10 Maths Question 3.
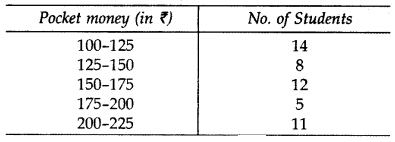
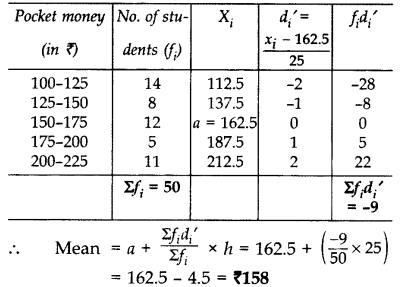
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f.

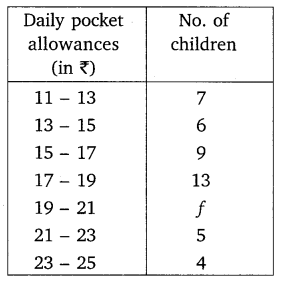
Solution:

Ex 14.1 Class 10 Maths Question 4.
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method

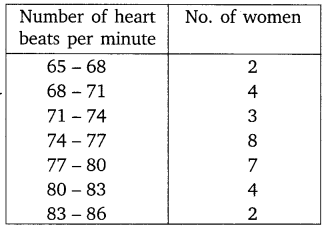
Solution:

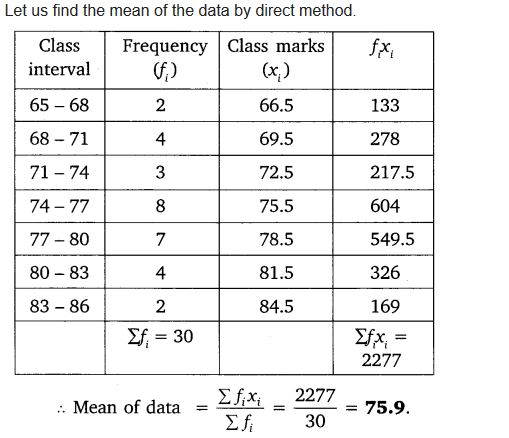
Ex 14.1 Class 10 Maths Question 5.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

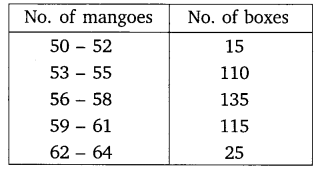
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:

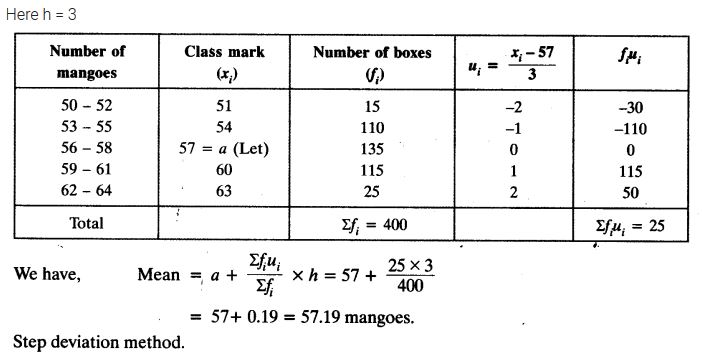
Ex 14.1 Class 10 Maths Question 6.
The table below shows the daily expenditure on food of 25 households in a locality.

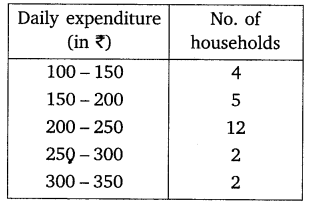
Find the mean daily expenditure on food by a suitable method.
Solution:

Ex 14.1 Class 10 Maths Question 7.
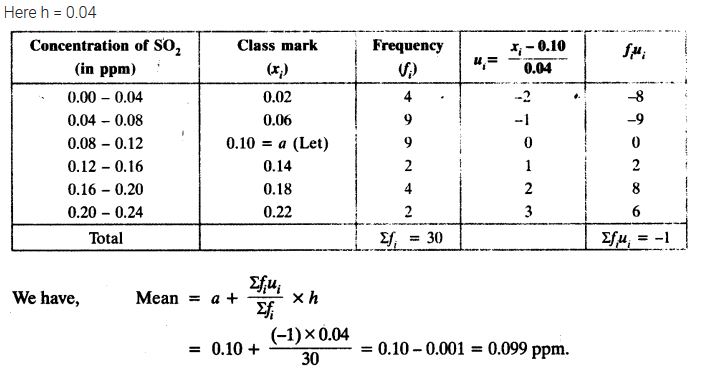
To find out the concentration of SO2 in the air (in parts per million, i.e. ppm), the data was collected for 30 localities in a certain city and is presented below:

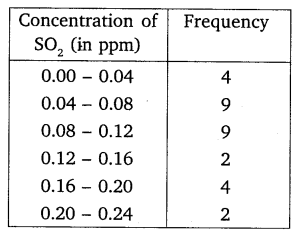
Find the mean concentration of SO2 in the air.
Solution:

Ex 14.1 Class 10 Maths Question 8.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

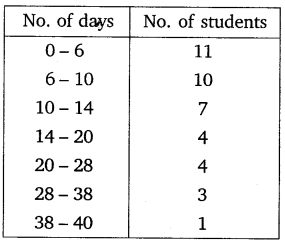
Solution:

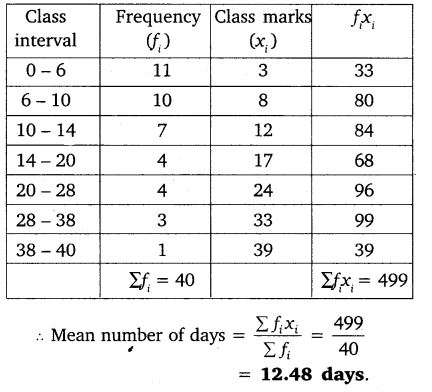
Ex 14.1 Class 10 Maths Question 9.
The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.

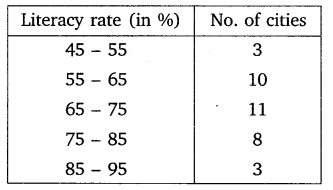
Solution:

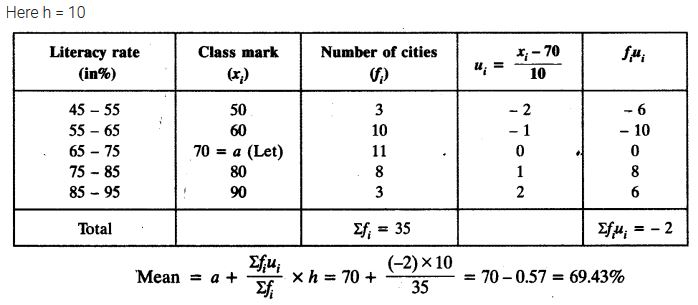
Class 10 Maths Statistics Mind Maps

Basic Terms

Class limits : Suppose mark obtained by all of the students are divided into class intervals 25 – 35, 35 – 45 and so interval on.
In class interval 25 – 35, 25 is called lower class limit and 35 is called upper class limit.
Class size : The difference between upper and lower class limit.
Class mark : It is given by

Ungrouped and Grouped Data

The data obtained in original form are called raw data or ungrouped data.
To put the data in a more condensed form, we make groups of suitable size, and mention the frequency of each group. Such a table is called grouped data.

Mean

For Ungrouped:
Consider ‘n’ observations in ungrouped data as : x₁, x₂, x₃, …. x_n. The mean of these observations is:

(i) Direct method:

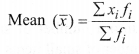
where ‘f_i‘ is the frequency corresponding to the class mark ‘x_i‘
(ii) Assumed mean method:

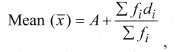
Where A is assumed mean and d_i = x_i – A
(iii) step deviation method:

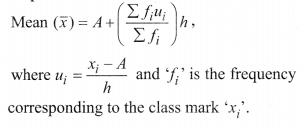
Mode

(i) For Ungrouped Data:
The mode is that observation which occurs most frequently, i.e., an observation with maximum frequency.
(ii) For Grouped Data:

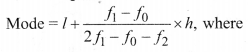
l =lower limit of the modal class,
f₁ = frequency of the modal class
f ₂ = frequency of the class suceeding the modal class,
h = size of the class interval,
f₀ = frequency of the class preceeding the modal class.
The class with the maximum frequency is called modal class.

Median

Median is a measure of central tendency which gives the value of the middle-most observation in the data.
(i) For Ungrouped Data:
Arrange the data in ascending order.
If number of data n is odd, then the median is (n+1/2)th observation.
If number of data n is even, then the median is the average of (n/2)th and (n/2+1)th observations.

(ii) For Grouped Data:

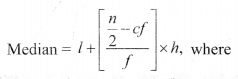
l = lower limit of the median class,
c.f = cumulative frequency of the class proceeding the median class,
f = frequency of the median class,
h = class size,
n = number of observations.
The class whose cumulative frequency is greater than (and nearest to) n/2 is called median class.

Relationship Between Mean, Mode and Median
3 Median = Mode + 2 Mean

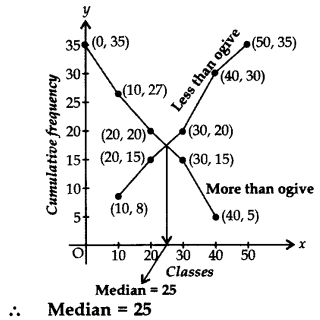
Cumulative Frequency Curve (Ogive)

(i) The smooth free hand curve is formed by joining the points (x_i, f_i) where x; is the upper limit of a class and f is the corresponding c.f. The curve so obtained is called a cumulative frequency curve, or an ogive of the less than type.
(ii) The smooth free hand curve is formed by joining the points (x_i, f_i) where X_i is the lower limit of a class and f is the corresponding c.f. The curve so obtained is called a cumulative frequency curve, or an ogive of the more than type.

Median by Graph

(i) Draw the ogive of the less than type and ogive of the more than type on the same axis. The two ogives will intersect each other at a point. From this point, if we draw a perpendicular on the x-axis, the point at which it cuts the x-axis gives us the median.
(ii) Draw the ogive of the less than type, then locate n/2 on the y-axis (n = number of observations).

From this point on y-axis, draw a line parallel to x-axis cutting the less than ogive at a point. From this point draw a perpendicular on the x-axis, the point at which the perpendicular cuts the x-axis gives us the median.

NCERT Solutions For Class 10 Maths Chapter 14 Statistics Ex 14.2

Ex 14.2 Class 10 Maths Question 1.
The following table shows the ages of the patients admitted in a hospital during a year.

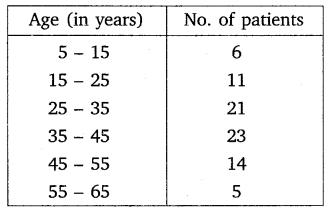
Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:

Ex 14.2 Class 10 Maths Question 2.
The following data gives information on the observed lifetimes (in hours) of 225 electrical components:

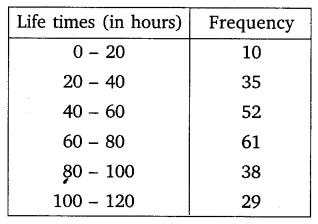
Determine the modal lifetimes of the components.
Solution:

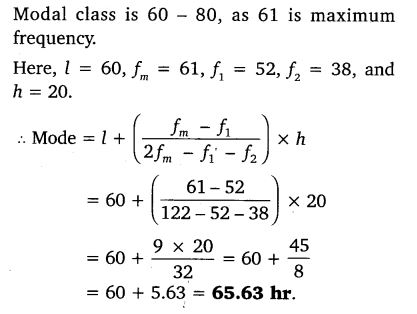
Ex 14.2 Class 10 Maths Question 3.
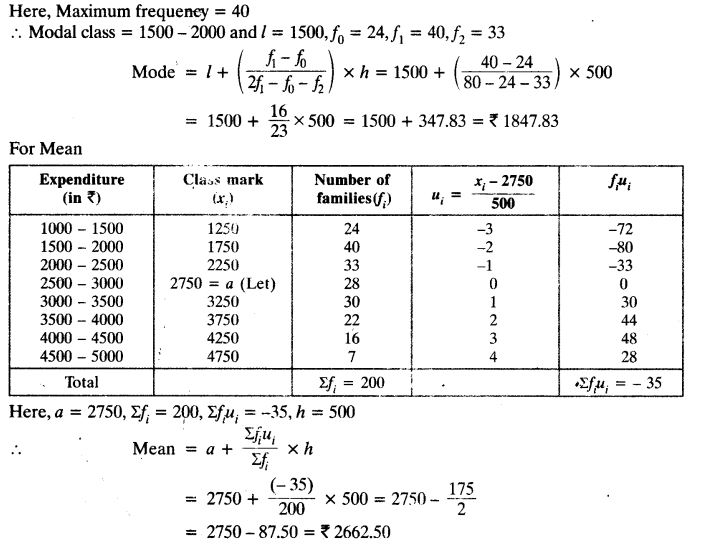
The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:

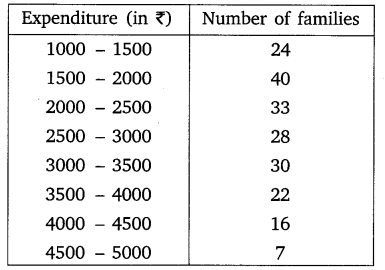
Solution:

Ex 14.2 Class 10 Maths Question 4.
The following distribution gives the state-wise teacher- student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.

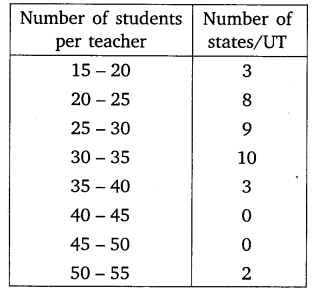
Solution:

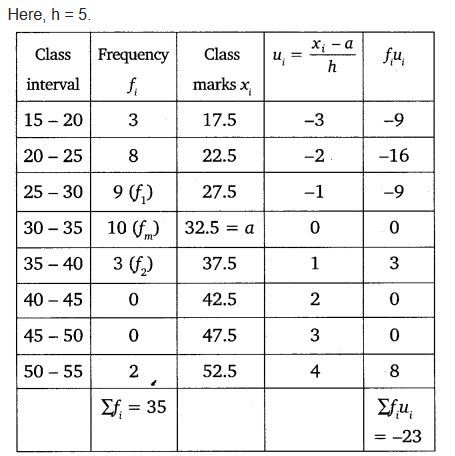
Ex 14.2 Class 10 Maths Question 5.
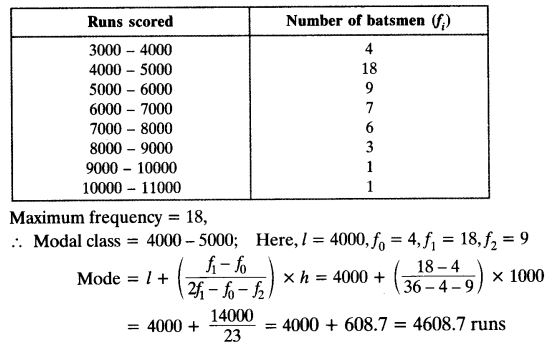
The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.

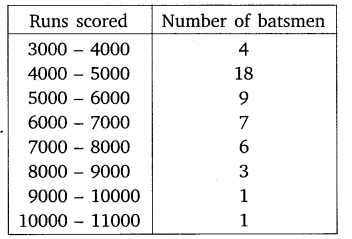
Find the mode of the data.
Solution:

Ex 14.2 Class 10 Maths Question 6.
A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data:

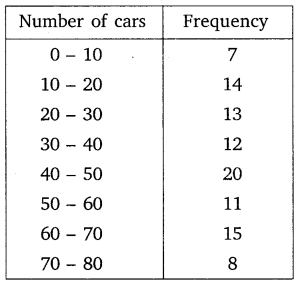
Solution:

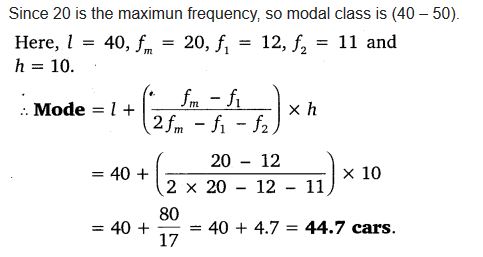
NCERT Solutions For Class 10 Maths Chapter 14 Statistics Ex 14.3

Ex 14.3 Class 10 Maths Question 1.
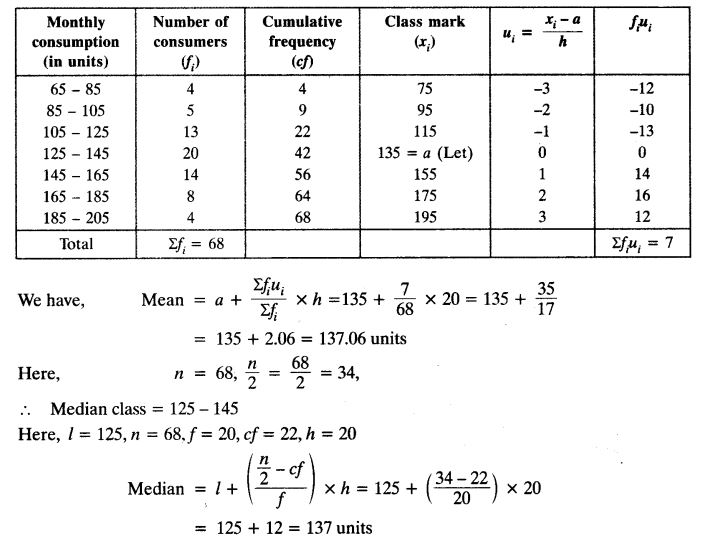
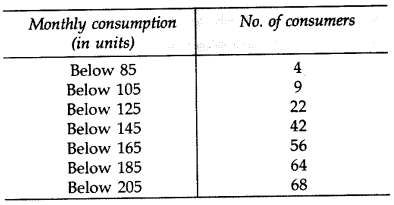
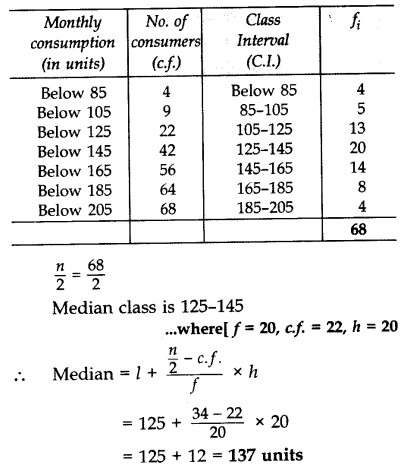
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

Solution:

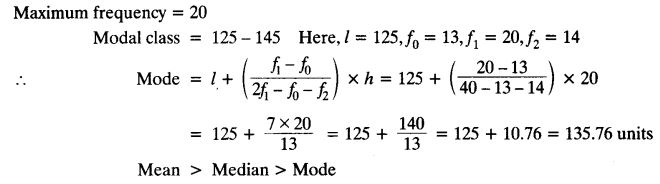
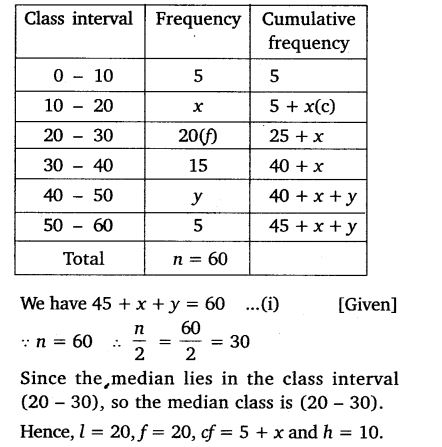
Ex 14.3 Class 10 Maths Question 2.
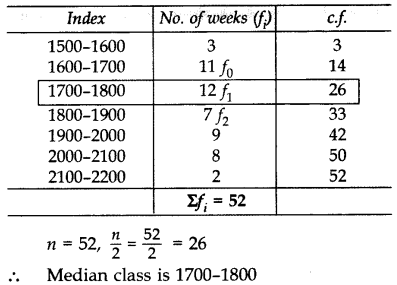
If the median of the distribution given below is 28.5, find the values of x and y.

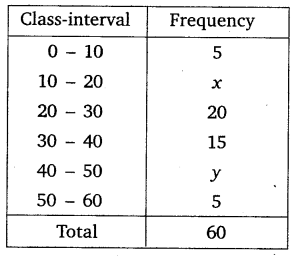
Solution:

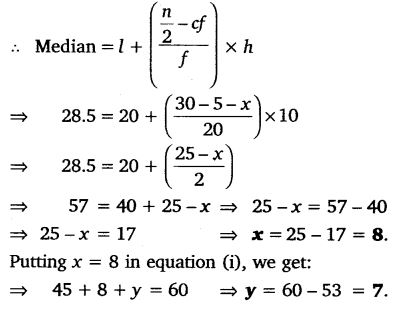
Ex 14.3 Class 10 Maths Question 3.
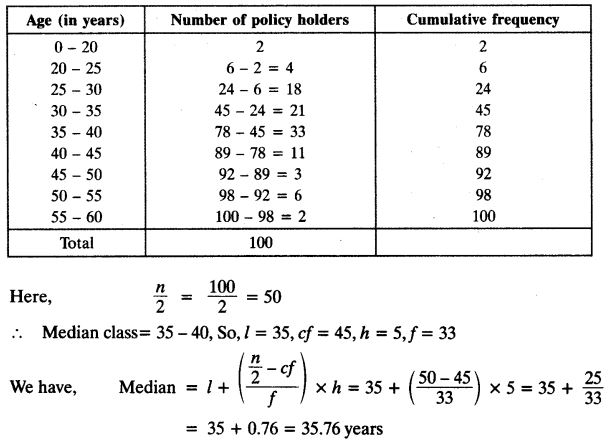
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.

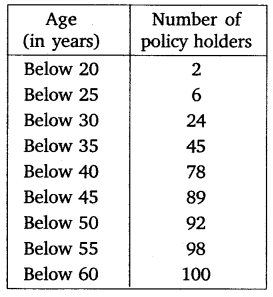
Solution:

Ex 14.3 Class 10 Maths Question 4.
The lengths of 40 leaves of a plant are measured correct to nearest millimetre, and the data obtained is represented in the following table:

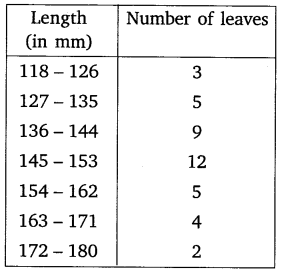
Find the median length of the leaves.
Solution:

Ex 14.3 Class 10 Maths Question 5.
The following table gives the distribution of the lifetime of 400 neon lamps:

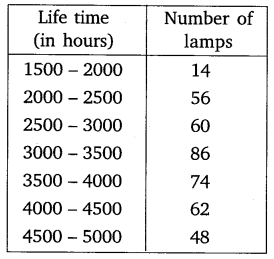
Find the median lifetime of a lamp.
Solution:

Ex 14.3 Class 10 Maths Question 6.
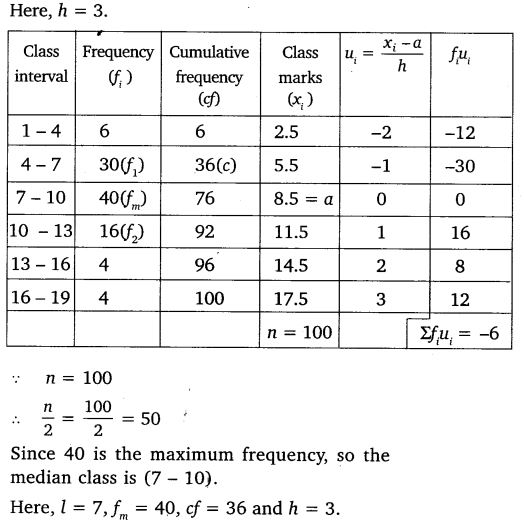
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabet in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames.
Solution:

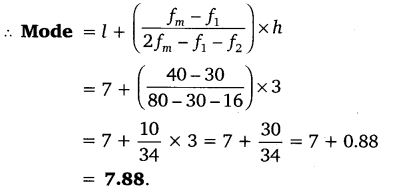
Ex 14.3 Class 10 Maths Question 7.
The distribution below gives the weight of 30 students of a class. Find the median weight of the students.

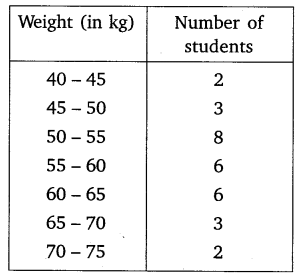
Solution:

NCERT Solutions For Class 10 Maths Chapter 14 Statistics Ex 14.4

Ex 14.4 Class 10 Maths Question 1.
The following distribution gives the daily income of 50 workers of a factory.

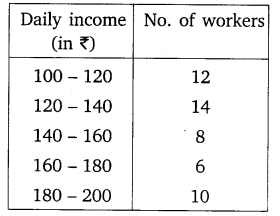
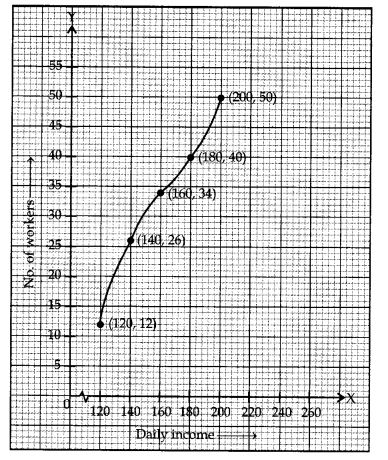
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:

Ex 14.4 Class 10 Maths Question 2.
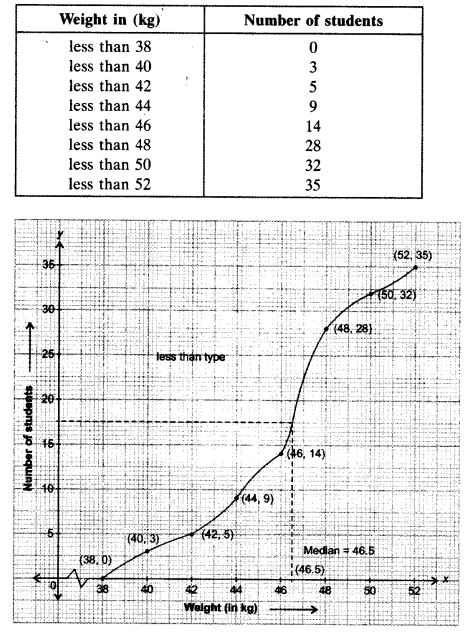
During the medical check-up of 35 students of a class, their weights were recorded as follows:

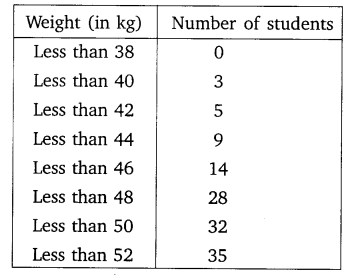
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:

Ex 14.4 Class 10 Maths Question 3.
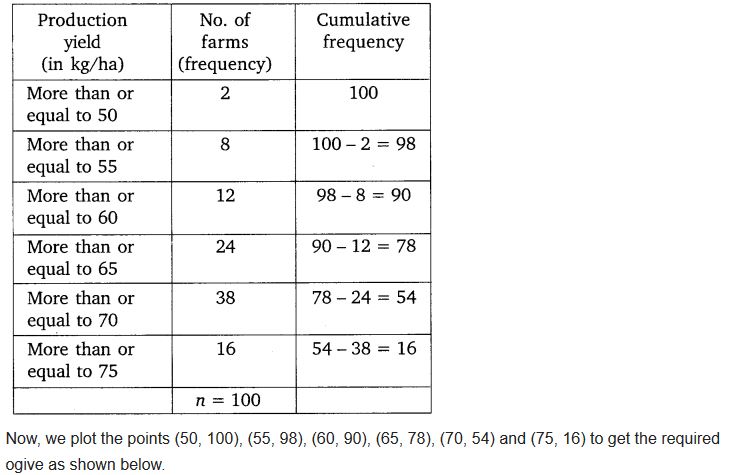
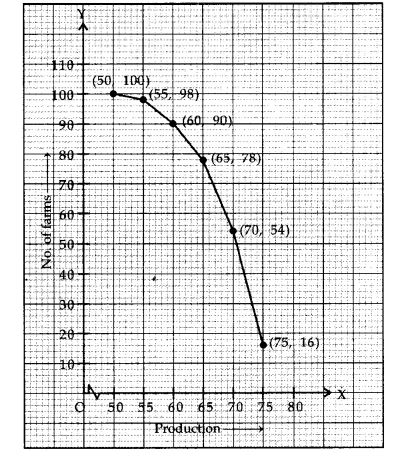
The following table gives production yield per hectare of wheat of 100 farms of a village.

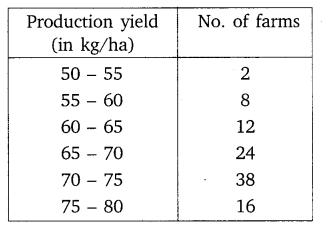
Change the distribution to a more than type distribution, and draw its ogive.
Solution:

Statistics Class 10 Extra Questions Maths Chapter 14

Important Questions for Class 10 Maths Chapter 14 Statistics

Statistics Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
In a continuous frequency distribution, the median of the data is 21. If each observation is increased by 5, then find the new median. (2015)
Solution:
New median = 21 + 5 = 26

Question 2.
From the following frequency distribution, find the median class: (2015)

Solution:

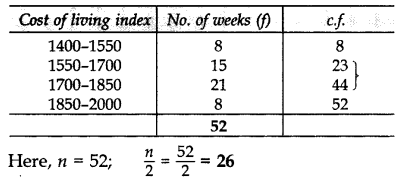
∴ Median class 1700 – 1850.

Question 3.
Consider the following distribution, find the frequency of class 30-40. (2013)

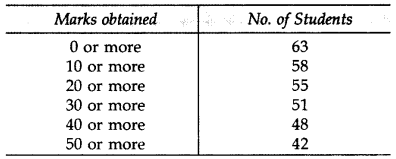
Solution:

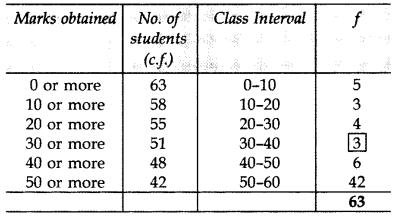
∴ Frequency of class 30 – 40 = 3

Question 4.
Following table shows sale of shoes in a store during one month: (2014)

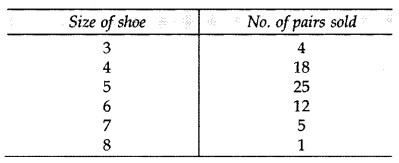
Find the model size of the shoes sold.
Solution:
Maximum no. of pairs sold = 25 (size 5)
∴ Modal size of shoes = 5

Question 5.
Weekly household expenditure of families living in a housing society are shown below: (2014)

Find the upper limit of the modal class.
Solution:
Maximum frequency = 48
∴ Modal class = 9,000 – 12,000
Upper limit of the modal class = 12,000

Statistics Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
The mean of the following data is 18.75. Find the value of P: (2012, 2017D)

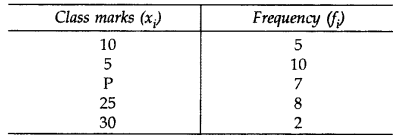
Solution:

Question 7.
Data regarding heights of students of Class X of Model School, Dehradun is given below. Calculate the average height of students of the class. (2015)

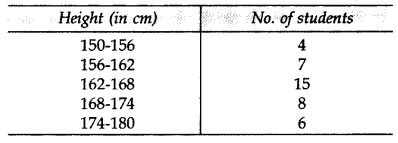
Solution:

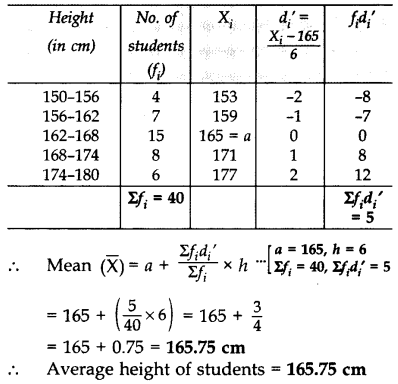
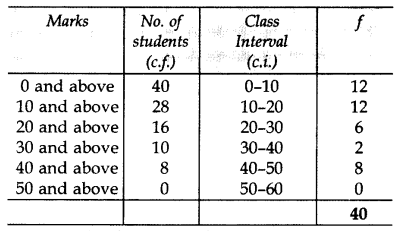
Question 8.
From the following cumulative frequency table, construct a frequency distribution table: (2013)

Solution:

Question 9.
Convert the following frequency distribution to a ‘more than’ type cumulative frequency distribution. (2012)

Solution:

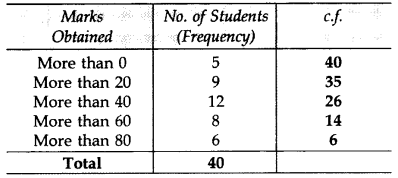
Question 10.
The distribution given below gives the daily income of 50 workers in a factory: (2017D)

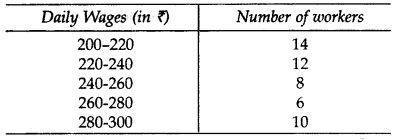
Convert the above distribution to a less than type cumulative frequency distribution.
Solution:

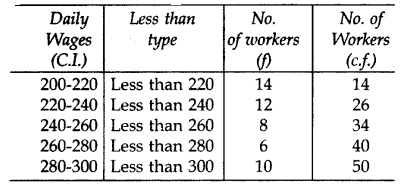
Question 11.
Find the mode of the following frequency distribution: (2013)

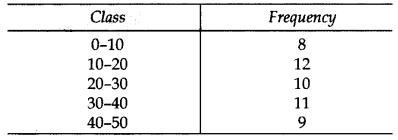
Solution:

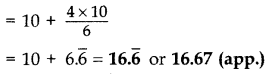
Question 12.
Given below is the distribution of weekly pocket money received by students of a class. Calculate the pocket money that is received by most of the students. (2014)

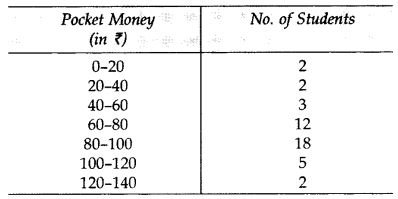
Solution:

∴ Required pocket money = ₹86.32 (approx.)

Question 13.
Find the median of the data using an empirical formula, when it is given that mode = 35.3 and mean = 30.5. (2014)
Solution:
Mode = 3(Median) – 2(Mean)
35.3 = 3(Median) – 2(30.5)
35.3 = 3(Median) – 61
96.3 = 3 Median
Median = 96.3/3 = 32.1

Question 14.
Show that the mode of the series obtained by combining the two series S₁ and S₂ given below is different from that of S₁ and S₂ taken separately: (2015)
S₁ : 3, 5, 8, 8, 9, 12, 13, 9, 9
S₂ : 7, 4, 7, 8, 7, 8, 13
Solution:
In S₁ : Number 9 occurs 3 times (maximum)
∴ Mode of S₁ Series = 9
In S₂ : Number 7 occurs 3 times (maximum)
∴ Mode of S, Series = 7
After combination:
In S₁ & S₂ : No. 8 occurs 4 times (maximum)
∴ Mode of S₁ & S₂ taken combined = 8
So, mode of S₁ & S₂ combined is different from that of S₁ & S₂ taken separately.

Statistics Class 10 Important Questions Short Answer-II (3 Marks)

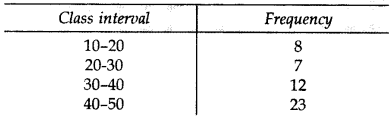
Question 15.
Find the mean of the following data. (2012)

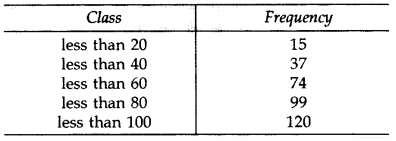
Solution:

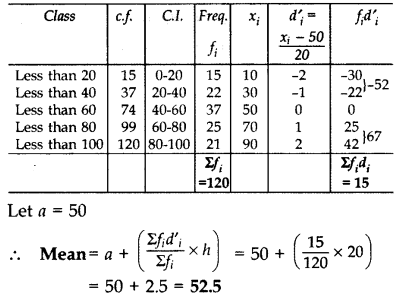
Question 16.
The following table gives the literacy rate (in %) in 40 cities. Find the mean literacy rate: (2012)

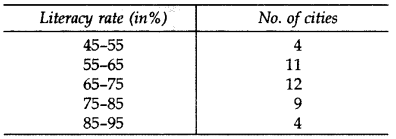
Solution:

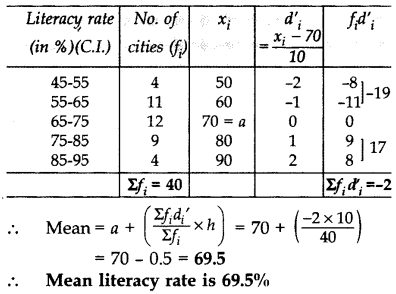
Question 17.
If the mean of the following distribution is 50, find the value of p: (2013)

Solution:

Question 18.
The mean of the following frequency distribution is 62.8. Find the missing frequency x. (2013)

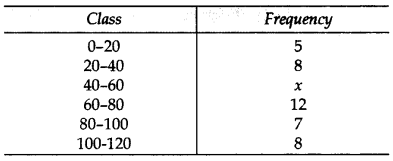
Solution:

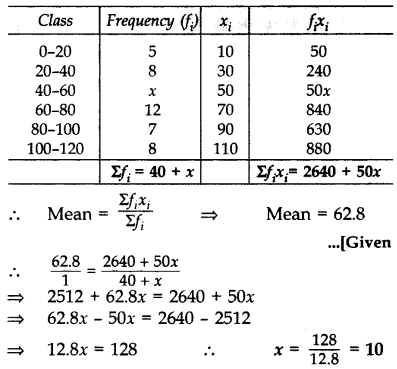
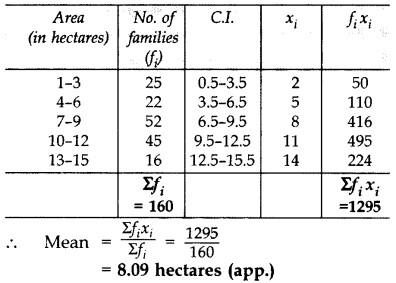
Question 19.
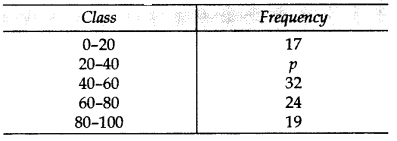
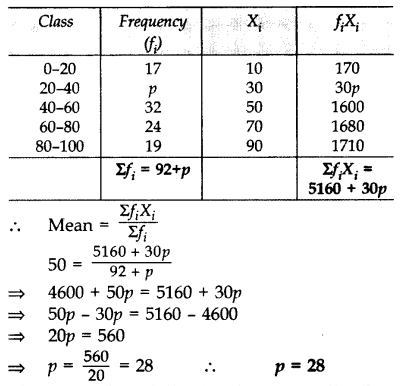
The frequency distribution table of agricultural holdings in a village is given below: (2013)

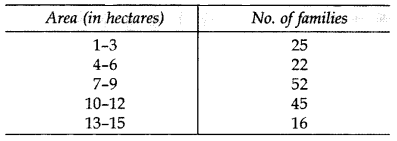
Find the Mean area held by a family.
Solution:

Question 20.
Monthly pocket money of students of a class is given in the following frequency distribution:

Find mean pocket money using step deviation method. (2014)
Solution:

Question 21.
Find the mean of the following distribution by Assumed Mean Method: (2015)


Solution:

Question 22.
Find the mean and median for the following data: (2015)

Solution:

Question 23.
For helping poor girls of their class, students saved pocket money as shown in the following table: (2014)

Find mean and median for this data.
Solution:

Question 24.
Weekly income of 600 families is given below:

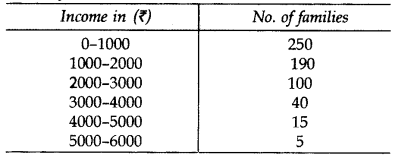
Find the median. (2012)
Solution:

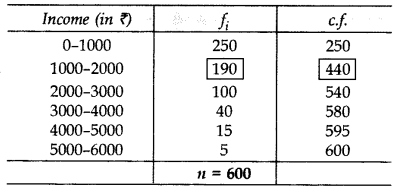
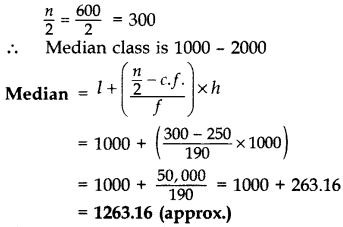
Question 25.
Find the median for the following distribution: (2013)

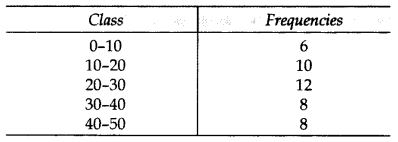
Solution:

Question 26.
Heights of students of class X are given in the following frequency distribution: (2014)

Find the modal height.
Solution:

Maximum frequency is 20
∴ Modal class is 160 – 165

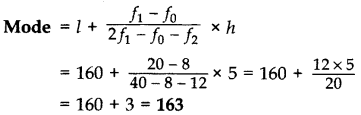
∴ The modal height = 163 cm

Question 27.
A medical camp was held in a school to impart health education and the importance of excercise to children. During this camp, a medical check of 35 students was done and their weights were recorded as follows: (2016)

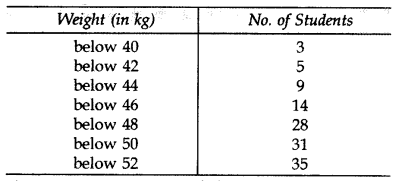
Compute the modal weight.
Solution:

∴ Modal weight = 46.9 kg

Question 28.
The average score of boys in the examination of a school is 71 and that of the girls is 73. The average score of the school in the examination is 71.8. Find the ratio of number of boys to the number of girls who appeared in the examination. (2015)
Solution:
Let the number of boys = n₁
and number of girls = n₂


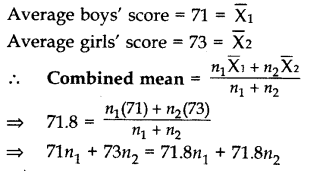
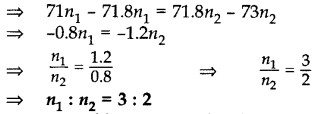
∴ No. of boys : No. of girls = 3 : 2

Question 29.
Following is the age distribution of dengue patients admitted in a hospital during a week of October, 2013: (2014)

Draw a ‘less than type’ ogive for the above distribution. Also, obtain median from the curve.
Solution:

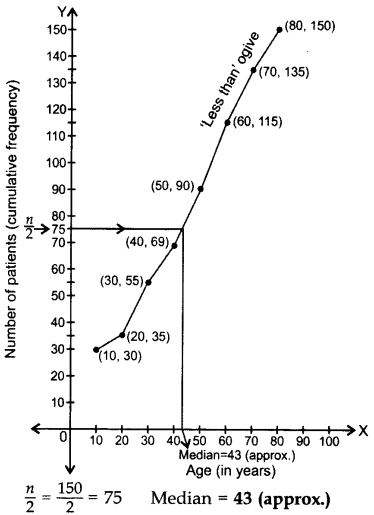
Question 30.
The lengths of leaves of a plant are measured correct to the nearest mm and the data obtained is represented as the following frequency distribution: (2015)


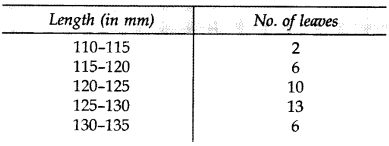
Draw a ‘more than type’ ogive for the above data.
Solution:

Statistics Class 10 Important Questions Long Answer (4 Marks)

Question 31.
The mean of the following frequency distribu tion is 53. But the frequencies f₁ and f₂ in the classes 20-40 and 60-80 are missing. Find the missing frequencies: (2013)

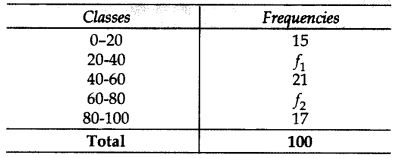
Solution:

⇒ 2730 + 30f₁ + 70f₂ = 5300
⇒ 30f₁ + 70f₂ = 5300 – 2730 = 2570
⇒ 3f₁ + 7f₂ = 257 …[Dividing by 10
⇒ 3f₁ +7(47 – f₁) = 257 . [From (i)
⇒ 3f₁ + 329 – 7f₁ = 257
⇒ -4f₁ = 257 – 329 = -72
⇒ f₁ = −72/−4 = 18
Putting the value of f₁ in (i), we get
f₂ = 47 – f₁
⇒ f₂ = 47 – 18 = 29
∴ f₁ = 18, f₂ = 29

Question 32.
The mean of the following frequency distribution is 62.8 and the sum of frequencies is 50. Find the missing frequencies f₁ and f₂: (2013)

Solution:

⇒ 2060 + 30f₁ + 70f₂ = 3140
⇒ 30f₁ + 70f₂ = 3140 – 2060 = 1080
⇒ 3f₁ + 7f₂ = 108 …[Dividing by 10
⇒ 3f₁ + 7(20 – f₁) = 108 … [From (i)
⇒ 3f₁ + 140 – 7f₁ = 108
⇒ -4f₁ = 108 – 140 = -32 .
∴ f₁ = 8
Putting the value of f₁ into (i), we get
f₂ = 20 – 8 = 12
∴ f₂ = 12

Question 33.
In the table below, heart-beats of 30 women are recorded. If mean of the data is 76, find the missing frequencies x and y. (2014)

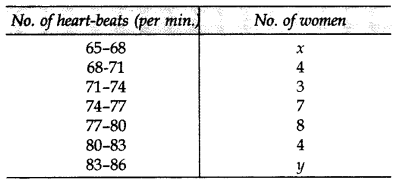
Solution:

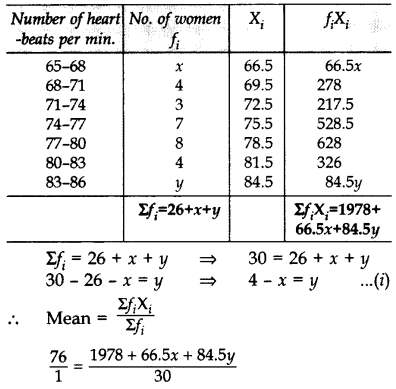
⇒ 1978 + 66.5x + 84.5y = 2280
⇒ 1978 + 66.5x + 84.5(4 – x) = 2280 … [From (i)
⇒ 1978 + 66.5x + 338 – 84.5x = 2280
⇒ 1978 + 338 – 2280 = 84.5x – 66.5x
⇒ 36 = 18x ⇒ x = 2
From (i), y = 4 – x = 4 – 2 = 2 ∴ x = 2, y = 2

Question 34.
The following table gives the daily income of 50 workers of a factory. Draw both types (“less than type” and “greater than type”) ogives. (2015)

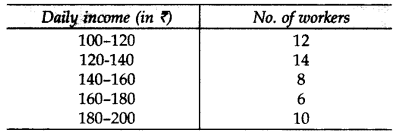
Solution:

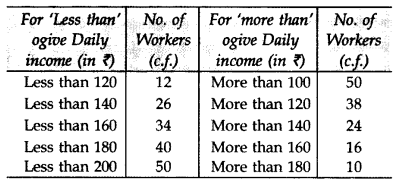
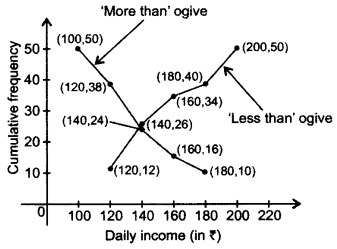
Question 35.
Find the values of x and y if the median for the following data is 31. (2012)

Solution:

⇒ 18 – x = (9 – x)10
⇒ 18 – x = 90 – 10x
⇒ -x + 10x = 90 – 18
⇒ 9x = 72
⇒ x = 8
Putting the value of x in (i), we have
y = 18 – 8 = 10
∴ x = 8, y = 10

Question 36.
The median of the following data is 525. Find x and y if the sum of all frequencies is 100: (2012, 2017 D)

Solution:

Question 37.
Find the missing frequencies f₁ and f₂ in the following frequency distribution table, if N = 100 and median is 32. (2013)

Solution:

Question 38.
Find the median of the following data: (2013)

Solution:

Question 39.
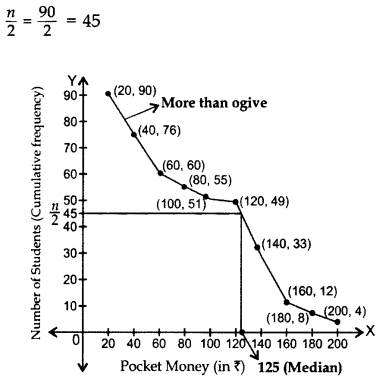
The frequency distribution of weekly pocket money received by a group of students is given below: (2014)

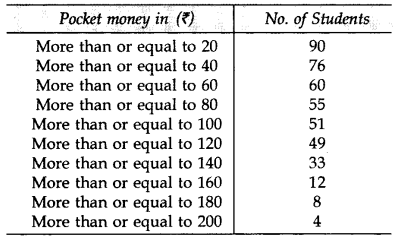
Draw a ‘more than type’ ogive and from it, find median. Verify median by actual calculations.
Solution:
n = 90 …[Given

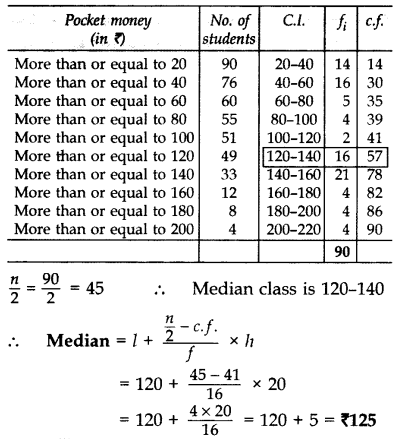
Question 40.
Draw “less than ogive” and “more than ogive” for the following distribution and hence find its median. (2012)

Solution:

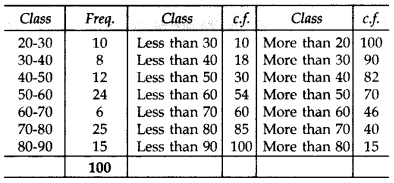
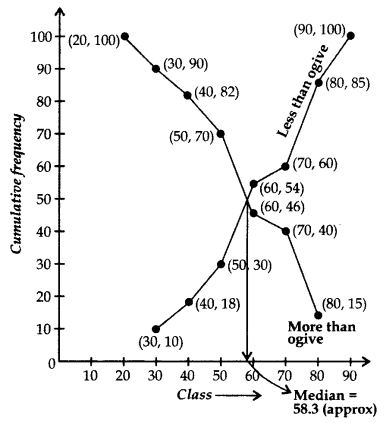
Question 41.
Draw: (a) more than ogive and (2017OD)
(b) less than ogive for the following data
Also find its median.

Solution:

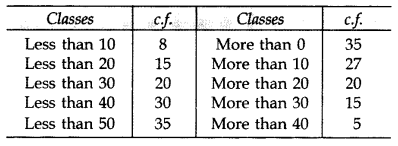
Question 42.
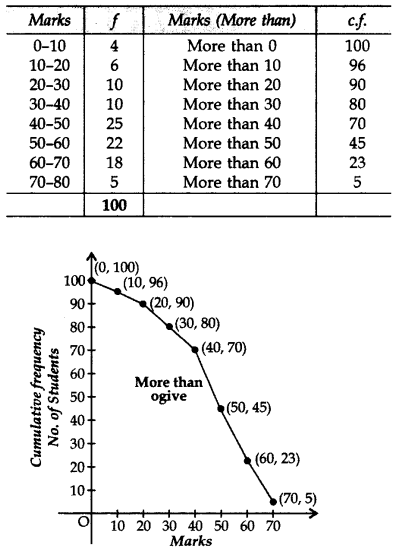
Draw a more than ogive for the data given below which gives the marks of 100 students: (2012, 2017D)

Solution:

Question 43.
For the following distribution, draw a ‘more than Ogive’ and hence find the median: (2013)

Solution:

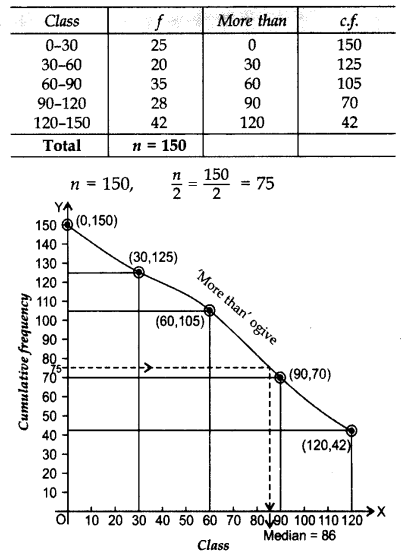
Question 44.
School held sports day in which 150 students participated. Ages of students are given in the following frequency distribution: (2014)

For the above data, draw a ‘more than type’ ogive and from the curve, find median. Verify it by actual calculations.
Solution:

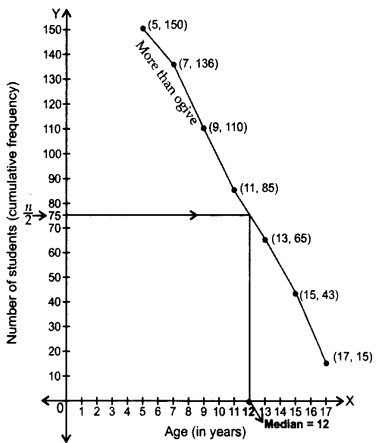
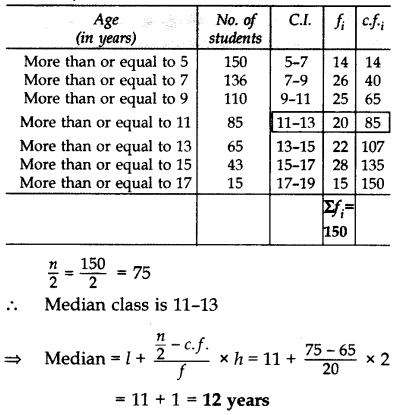
Question 45.
In a class test, marks obtained by 120 students are given in the following frequency distribution. If it is given that mean is 59, find the missing frequencies x and y. (2015)

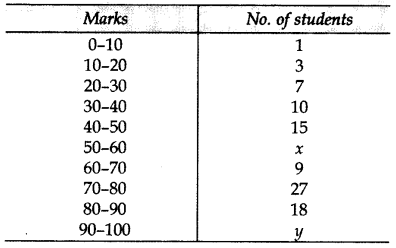
Solution:

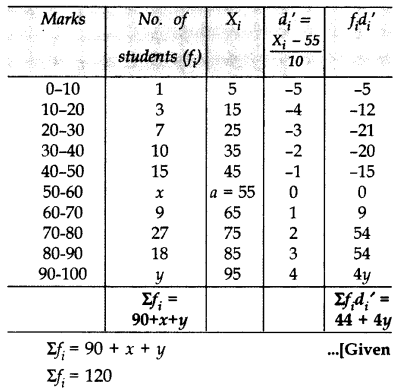
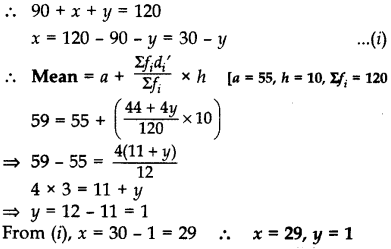
Question 46.
Mode of the following frequency distribution is 65 and sum of all the frequencies is 70. Find the missing frequencies x and y. (2015)

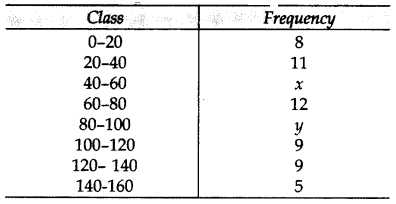
Solution:

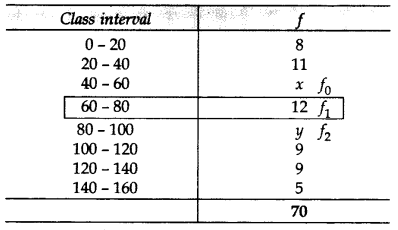
54 + x + y = 70 … [Given
x + y = 70 – 54 = 16 …(i)
∴ Mode = 65
Modal Class is 60 – 80

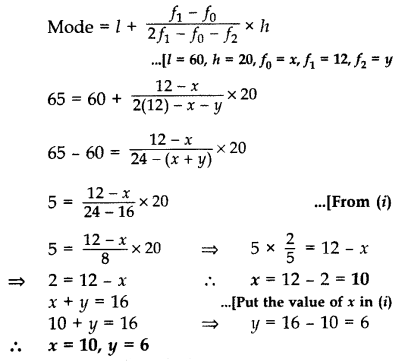
Question 47.
Find the mode of the following frequency distribution: (2015)

Solution:

Question 48.
Cost of Living Index for some period is given in the following frequency distribution: (2014)

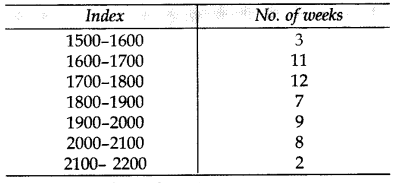
Find the mode and median for above data.
Solution:

CBSE Class 10 Maths Notes Chapter 14 Statistics

MEAN (AVERAGE): Mean [Ungrouped Data] – Mean of n observations, x₁, x₂, x₃ … x_n, is

MEAN [Grouped Data]: The mean for grouped data can be found by the following three methods:
(i) Direct Mean Method:

Class Mark = Upper Class Limit + Lower Class Limit / 2

Note: Frequency of a class is centred at its mid-point called class mark.

(ii) Assumed Mean Method: In this, an arbitrary mean ‘a’ is chosen which is called, ‘assumed mean’, somewhere in the middle of all the values of x.

…[where d_i = (x_i – a)]

(iii) Step Deviation Method:

….. [where ui=di/h , where h is a common divisor of d_i]

MEDIAN: Median is a measure of central tendency which gives the value of the middle-most observation in the data.

…where[l = Lower limit of median class; n = Number of observations; f = Frequency of median class; c.f. = Cumulative frequency of preceding class; h = Class size]

(iii) Representing a cumulative frequency distribution graphically as a cumulative frequency curve, or an ogive of the less than type and of the more than type. The median of grouped data can be obtained graphically as the x-coordinate of the point of intersection of the two ogives for this data.

Mode:
(i) Ungrouped Data: The value of the observation having maximum frequency is the mode.
(ii) Grouped Data:

…where[l = Lower limit of modal class; f₁ = Frequency of modal class; f₀ = Frequency of the class preceding the modal class; f₂ = Frequency of the class succeeding the modal class; h = Size of class interval. c.f. = Cumulative frequency of preceding class; h = Class size]

Mode = 3 Median – 2 Mean
Median = Mode+2Mean/3
Mean = 3Median−Mode/2