NCERT Solutions For Class 10 Maths Chapter 2 Polynomials

NCERT Solutions For Class 10 Maths Chapter 2 Polynomials

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.1

Ex 2.1 Class 10 Maths Question 1:
The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each case.

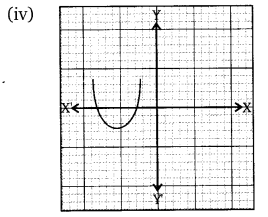
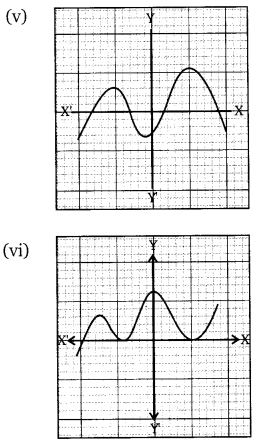
Solution:

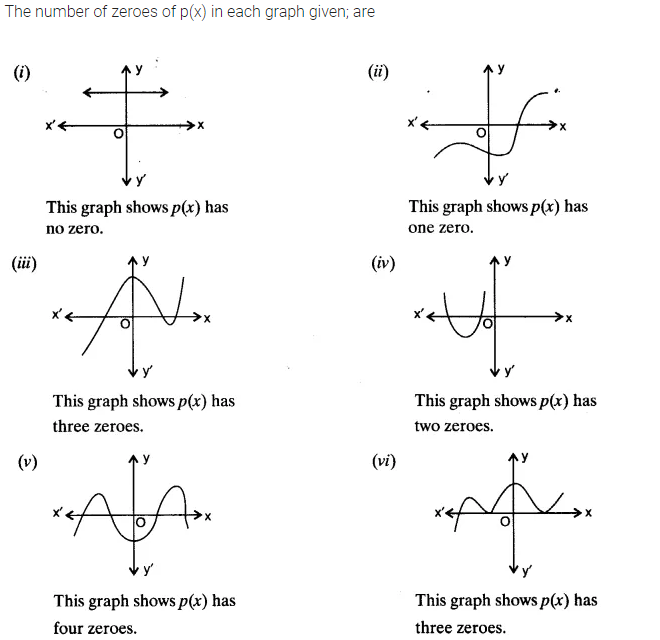
You can also download the free PDF of Ex 2.1 Class 10 Polynomials NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.2

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.2 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials Exercise 2.2.

Ex 2.2 Class 10 Maths Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
Solution:

Ex 2.2 Class 10 Maths Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:

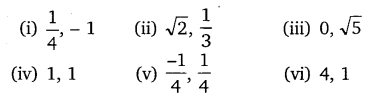
Solution:

NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.3

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials Exercise 2.3.
Ex 2.3 Class 10 Maths Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴– 5x + 6, g(x) = 2 – x^2
Solution:

Ex 2.3 Class 10 Maths Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t² – 3, 2t⁴ + 3t³ – 2t²– 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x² + 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:

Ex 2.3 Class 10 Maths Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are  and 53−−√ and –53−−√
Solution:

Ex 2.3 Class 10 Maths Question 4.
On dividing x³ – 3x² + x + 2bya polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:

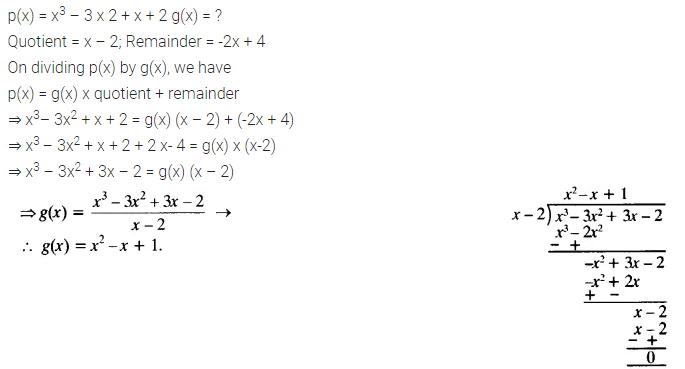
Ex 2.3 Class 10 Maths Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:

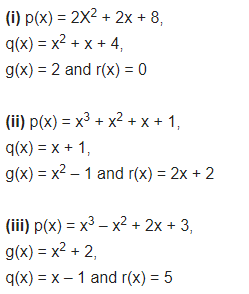
NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.4

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials Exercise 2.4.
Ex 2.4 Class 10 Maths Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x³ + x² – 5x + 2;  1/4, 1, -2
(ii) x³ – 4x² + 5x – 2; 2, 1, 1
Solution:

Ex 2.4 Class 10 Maths Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:

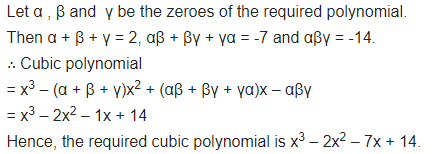
Ex 2.4 Class 10 Maths Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a-b, a, a + b, find a and b.
Solution:

Ex 2.4 Class 10 Maths Question 4.
If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Ex 2.4 Class 10 Maths Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:

Polynomials Class 10 Extra Questions Maths Chapter 2

Extra Questions for Class 10 Maths Chapter 2 Polynomials. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.

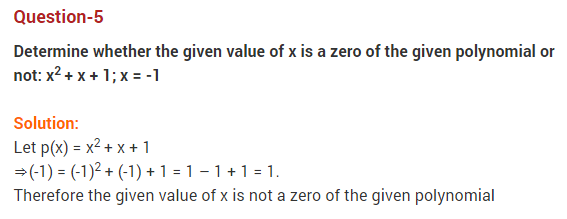
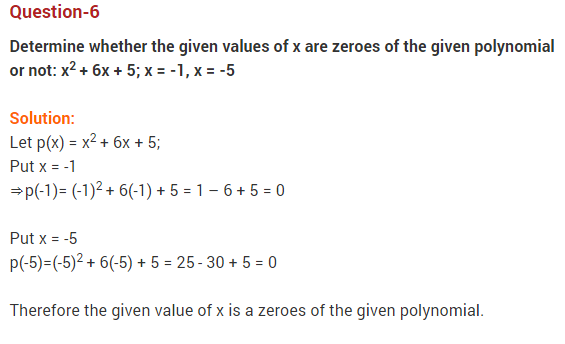
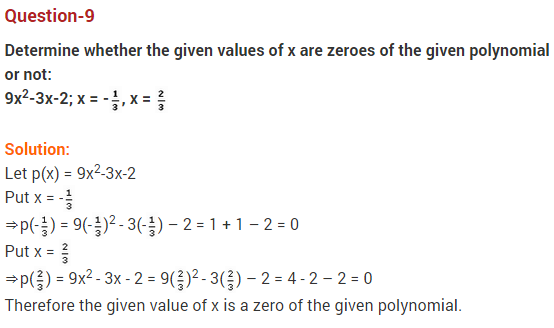
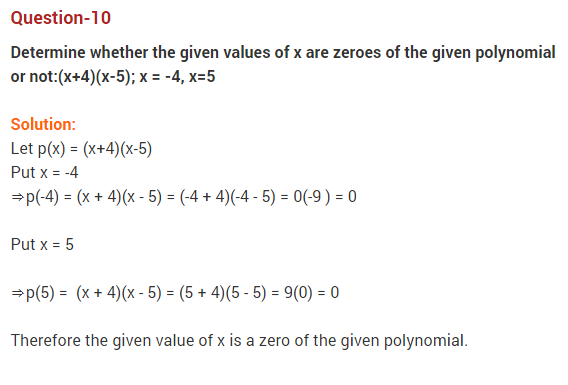
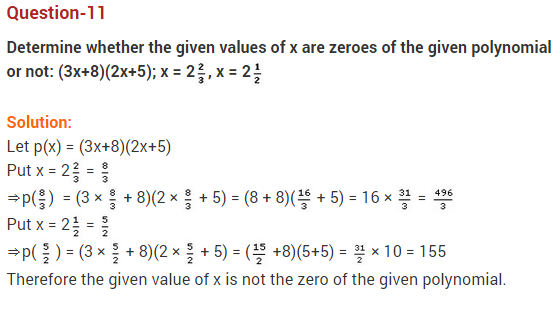
Important Questions for Class 10 Maths Chapter 2 Polynomials

Polynomials Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If the sum of zeroes of the quadratic polynomial 3x² – kx + 6 is 3, then find the value of k. (2012)
Solution:
Here a = 3, b = -k, c = 6
Sum of the zeroes, (α + β) = −b/a = 3 …..(given)
⇒ −(−k)/3 = 3
⇒ k = 9

Question 2.
If α and β are the zeroes of the polynomial ax² + bx + c, find the value of α² + β². (2013)
Solution:

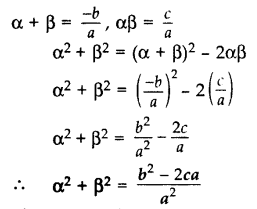
Question 3.
If the sum of the zeroes of the polynomial p(x) = (k² – 14) x² – 2x – 12 is 1, then find the value of k. (2017 D)
Solution:
p(x) = (k² – 14) x² – 2x – 12
Here a = k² – 14, b = -2, c = -12
Sum of the zeroes, (α + β) = 1 …[Given]
⇒ −b/a = 1
⇒ −(−2)/k2−14 = 1
⇒ k² – 14 = 2
⇒ k² = 16
⇒ k = ±4

Question 4.
If α and β are the zeroes of a polynomial such that α + β = -6 and αβ = 5, then find the polynomial. (2016 D)
Solution:
Quadratic polynomial is x² – Sx + P = 0
⇒ x² – (-6)x + 5 = 0
⇒ x² + 6x + 5 = 0

Question 5.
A quadratic polynomial, whose zeroes are -4 and -5, is …. (2016 D)
Solution:
x² + 9x + 20 is the required polynomial.

Polynomials Class 10 Important Questions Short Answer-I (2 Marks)

Question 6.
Find the condition that zeroes of polynomial p(x) = ax² + bx + c are reciprocal of each other. (2017 OD)
Solution:
Let α and 1/α be the zeroes of P(x).
P(a) = ax² + bx + c …(given)
Product of zeroes = c/a
⇒ α × 1/α = c/a
⇒ 1 = c/a
⇒ a = c (Required condition)
Coefficient of x² = Constant term

Question 7.
Form a quadratic polynomial whose zeroes are 3 + √2 and 3 – √2. (2012)
Solution:
Sum of zeroes,
S = (3 + √2) + (3 – √2) = 6
Product of zeroes,
P = (3 + √2) x (3 – √2) = (3)² – (√2)² = 9 – 2 = 7
Quadratic polynomial = x² – Sx + P = x² – 6x + 7

Question 8.
Find a quadratic polynomial, the stun and product of whose zeroes are √3 and 1/√3 respectively. (2014)
Solution:
Sum of zeroes, (S) = √3
Product of zeroes, (P) = 1/√3
Quadratic polynomial = x² – Sx + P

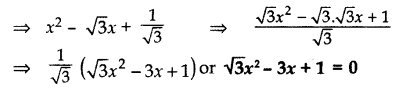
Question 9.
Find a quadratic polynomial, the sum and product of whose zeroes are 0 and -√2 respectively. (2015)
Solution:
Quadratic polynomial is
x² – (Sum of zeroes) x + (Product of zeroes)
= x² – (0)x + (-√2)
= x² – √2

Question 10.
Find the zeroes of the quadratic polynomial √3 x² – 8x + 4√3. (2013)
Solution:

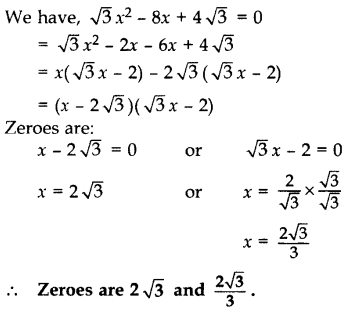
Question 11.
If the zeroes of the polynomial x² + px + q are double in value to the zeroes of 2x² – 5x – 3, find the value of p and q. (2012)
Solution:
We have, 2x² – 5x – 3 = 0
= 2x² – 6x + x – 3
= 2x(x – 3) + 1(x – 3)
= (x – 3) (2x + 1)
Zeroes are:
x – 3 = 0 or 2x + 1 = 0
⇒ x = 3 or x = −1/2
Since the zeroes of required polynomial is double of given polynomial.
Zeroes of the required polynomial are:
3 × 2, (−1/2 × 2), i.e., 6, -1
Sum of zeroes, S = 6 + (-1) = 5
Product of zeroes, P = 6 × (-1) = -6
Quadratic polynomial is x² – Sx + P
⇒ x² – 5x – 6 …(i)
Comparing (i) with x² + px + q
p = -5, q = -6

Question 12.
Can (x – 2) be the remainder on division of a polynomial p(x) by (2x + 3)? Justify your answer. (2016 OD)
Solution:
In case of division of a polynomial by another polynomial, the degree of the remainder (polynomial) is always less than that of the divisor. (x – 2) can not be the remainder when p(x) is divided by (2x + 3) as the degree is the same.

Question 13.
Find a quadratic polynomial whose zeroes are 3+√5/5 and 3−√5/5. (2013)
Solution:

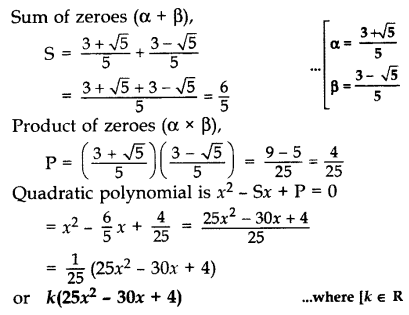
Question 14.
Find the quadratic polynomial whose zeroes are -2 and -5. Verify the relationship between zeroes and coefficients of the polynomial. (2013)
Solution:
Sum of zeroes, S = (-2) + (-5) = -7
Product of zeroes, P = (-2)(-5) = 10
Quadratic polynomial is x² – Sx + P = 0
= x² – (-7)x + 10
= x² + 7x + 10
Verification:
Here a = 1, b = 7, c = 10
Sum of zeroes = (-2) + (-5) = 7

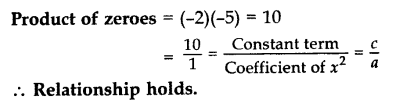
Question 15.
Find the zeroes of the quadratic polynomial 3x² – 75 and verify the relationship between the zeroes and the coefficients. (2014)
Solution:
We have, 3x² – 75
= 3(x² – 25)
= 3(x² – 52)
= 3(x – 5)(x + 5)
Zeroes are:
x – 5 = 0 or x + 5 = 0
x = 5 or x = -5
Verification:
Here a = 3, b = 0, c = -75
Sum of the zeroes = 5 + (-5) = 0

Question 16.
Find the zeroes of p(x) = 2x² – x – 6 and verify the relationship of zeroes with these co-efficients. (2017 OD)
Solution:
p(x) = 2x² – x – 6 …[Given]
= 2x² – 4x + 3x – 6
= 2x (x – 2) + 3 (x – 2)
= (x – 2) (2x + 3)
Zeroes are:
x – 2 = 0 or 2x + 3 = 0
x = 2 or x = −3/2
Verification:
Here a = 2, b = -1, c = -6

Question 17.
What must be subtracted from the polynomial f(x) = x⁴ + 2x³ – 13x² – 12x + 21 so that the resulting polynomial is exactly divisible by x² – 4x + 3? (2012, 2017 D)
Solution:

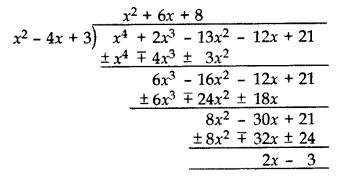
(2x – 3) should be subtracted from x⁴ + 2x³ – 13x² – 12x + 21.

Polynomials Class 10 Important Questions Short Answer-II (3 Marks)

Question 18.
Verify whether 2, 3 and 1/2 are the zeroes of the polynomial p(x) = 2x³ – 11x² + 17x – 6. (2012, 2017 D)
Solution:
p(x) = 2x³ – 11x² + 17x – 6
When x = 2,
p(2) = 2(2)³ – 11(2)² + 17(2) – 6 = 16 – 44 + 34 – 6 = 0
When x = 3, p(3) = 2(3)³ – 11(3)² + 17(3) – 6 = 54 – 99 + 51 – 6 = 0

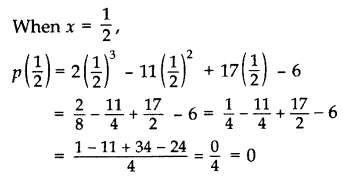
Yes, x = 2, 3 and 1/2 all are the zeroes of the given polynomial.

Question 19.
Show that 1/2 and −3/2 are the zeroes of the polynomial 4x² + 4x – 3 and verify the relationship between zeroes and co-efficients of polynomial. (2013)
Solution:
Let P(x) = 4x² + 4x – 3

Question 20.
Find a quadratic polynomial, the sum and product of whose zeroes are -8 and 12 respectively. Hence find the zeroes. (2014)
Solution:
Let Sum of zeroes (α + β) = S = -8 …[Given]
Product of zeroes (αβ) = P = 12 …[Given]
Quadratic polynomial is x² – Sx + P
= x² – (-8)x + 12
= x² + 8x + 12
= x² + 6x + 2x + 12
= x(x + 6) + 2(x + 6)
= (x + 2)(x + 6)
Zeroes are:
x + 2 = 0 or x + 6 = 0
x = -2 or x = -6

Question 21.
Find a quadratic polynomial, the sum and product of whose zeroes are 0 and −3/5 respectively. Hence find the zeroes. (2015)
Solution:
Quadratic polynomial = x² – (Sum)x + Product

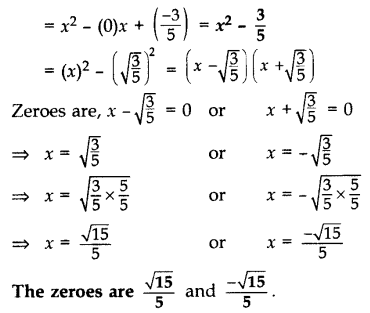
Question 22.
Find the zeroes of the quadratic polynomial 6x² – 3 – 7x and verify the relationship between the zeroes and the coefficients of the polynomial. (2015, 2016 OD)
Solution:
We have, 6x² – 3 – 7x
= 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (2x – 3) (3x + 1)

Question 23.
Find the zeroes of the quadratic polynomial f(x) = x² – 3x – 28 and verify the relationship between the zeroes and the co-efficients of the polynomial. (2012, 2017 D)
Solution:
p(x) = x² – 3x – 28
= x² – 7x + 4x – 28
= x(x – 7) + 4(x – 7)
= (x – 7) (x + 4)
Zeroes are:
x – 7 = 0 or x + 4 = 0
x = 7 or x = -4

Question 24.
If α and β are the zeroes of the polynomial 6y² – 7y + 2, find a quadratic polynomial whose zeroes are 1α and 1/β. (2012)
Solution:
Given: 6y² – 7y + 2
Here a = 6, b = -7, c = 2

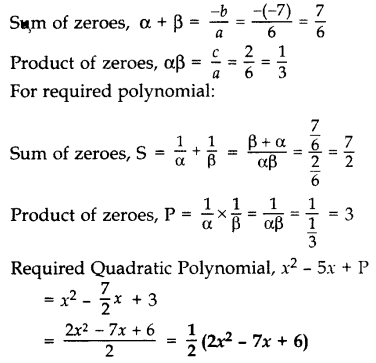
Question 25.
Divide 3x² + 5x – 1 by x + 2 and verify the division algorithm. (2013 OD)
Solution:

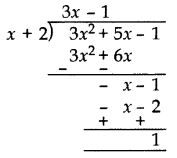
Quotient = 3x – 1
Remainder = 1
Verification:
Divisor × Quotient + Remainder
= (x + 2) × (3x – 1) + 1
= 3x² – x + 6x – 2 + 1
= 3x² + 5x – 1
= Dividend

Question 26.
On dividing 3x³ + 4x² + 5x – 13 by a polynomial g(x) the quotient and remainder were 3x +10 and 16x – 43 respectively. Find the polynomial g(x). (2017 OD)
Solution:
Let 3x³ + 4x² + 5x – 13 = P(x)
q(x) = 3x + 10, r(x) = 16x – 43 …[Given]
As we know, P(x) = g(x) . q(x) + r(x)
3x³ + 4x² + 5x – 13 = g(x) . (3x + 10) + (16x – 43)
3x³ + 4x² + 5x – 13 – 16x + 43 = g(x) . (3x + 10)

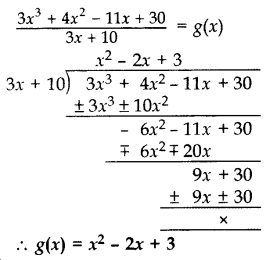
Question 27.
Check whether polynomial x – 1 is a factor of the polynomial x³ – 8x² + 19x – 12. Verify by division algorithm. (2014)
Solution:
Let P(x) = x³ – 8x² + 19x – 12
Put x = 1
P(1) = (1)³ – 8(1)² + 19(1) – 12
= 1 – 8 + 19 – 12
= 20 – 20
= 0
Remainder = 0
(x – 1) is a facter of P(x).
Verification:

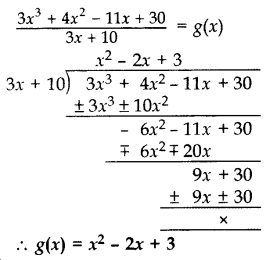
Since remainder = 0
(x – 1) is a factor of P(x).

Polynomials Class 10 Important Questions Long Answer (4 Marks)

Question 28.
Divide 4x³ + 2x² + 5x – 6 by 2x² + 1 + 3x and verify the division algorithm. (2013)
Solution:

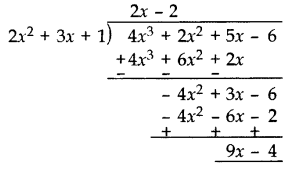
Quotient = 2x – 2
Remainder = 9x – 4
Verification:
Divisor × Quotient + Remainder
= (2x² + 3x + 1) × (2x – 2) + 9x – 4
= 4x³ – 4x² + 6x² – 6x + 2x – 2 + 9x – 4
= 4x³ + 2x² + 5x – 6
= Dividend

Question 29.
Given that x – √5 is a factor of the polynomial x³ – 3√5 x² – 5x + 15√5, find all the zeroes of the polynomial. (2012, 2016)
Solution:
Let P(x) = x³ – 3√5 x² – 5x + 15√5
x – √5 is a factor of the given polynomial.
Put x = -√5,

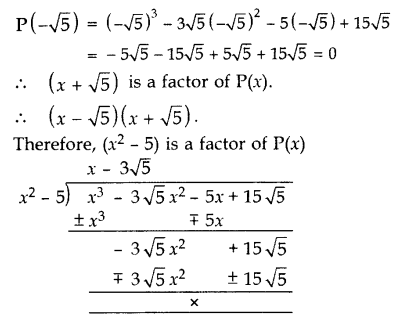
Other zero:
x – 3√5 = 0 ⇒ x = 3√5
All the zeroes of P(x) are -√5, √5 and 3√5.

Question 30.
If a polynomial x⁴ + 5x³ + 4x² – 10x – 12 has two zeroes as -2 and -3, then find the other zeroes. (2014)
Solution:
Since two zeroes are -2 and -3.
(x + 2)(x + 3) = x² + 3x + 2x + 6 = x² + 5x + 6
Dividing the given equation with x² + 5x + 6, we get

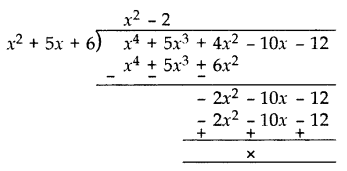
x⁴ + 5x³ + 4x² – 10x – 12
= (x² + 5x + 6)(x² – 2)
= (x + 2)(x + 3)(x – √2 )(x + √2 )
Other zeroes are:
x – √2 = 0 or x + √2 = 0
x = √2 or x = -√2

Question 31.
Find all the zeroes of the polynomial 8x⁴ + 8x³ – 18x² – 20x – 5, if it is given that two of its zeroes are √5/2 and −√5/2. (2014, 2016 D)
Solution:

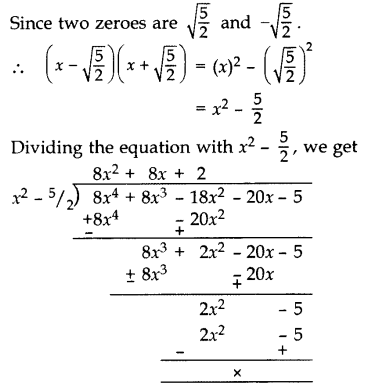
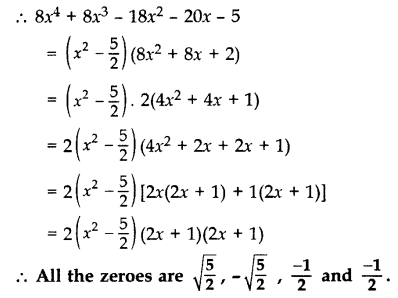
Question 32.
If p(x) = x³ – 2x² + kx + 5 is divided by (x – 2), the remainder is 11. Find k. Hence find all the zeroes of x³ + kx² + 3x + 1. (2012)
Solution:
p(x) = x³ – 2x² + kx + 5,
When x – 2,
p(2) = (2)³ – 2(2)² + k(2) + 5
⇒ 11 = 8 – 8 + 2k + 5
⇒ 11 – 5 = 2k
⇒ 6 = 2k
⇒ k = 3
Let q(x) = x³ + kx² + 3x + 1
= x³ + 3x² + 3x + 1
= x³ + 1 + 3x² + 3x
= (x)³ + (1)³ + 3x(x + 1)
= (x + 1)³
= (x + 1) (x + 1) (x + 1) …[∵ a³ + b³ + 3ab (a + b) = (a + b)³]
All zeroes are:
x + 1 = 0 ⇒ x = -1
x + 1 = 0 ⇒ x = -1
x + 1 = 0 ⇒ x = -1
Hence zeroes are -1, -1 and -1.

Question 33.
If α and β are zeroes of p(x) = kx² + 4x + 4, such that α² + β² = 24, find k. (2013)
Solution:
We have, p(x) = kx² + 4x + 4
Here a = k, b = 4, c = 4

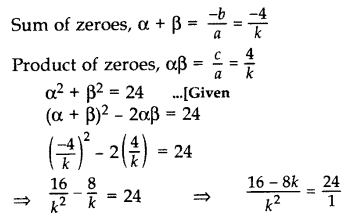
⇒ 24k² = 16 – 8k
⇒ 24k² + 8k – 16 = 0
⇒ 3k² + k – 2 = 0 …[Dividing both sides by 8]
⇒ 3k² + 3k – 2k – 2 = 0
⇒ 3k(k + 1) – 2(k + 1) = 0
⇒ (k + 1)(3k – 2) = 0
⇒ k + 1 = 0 or 3k – 2 = 0
⇒ k = -1 or k = 2/3

Question 34.
If α and β are the zeroes of the polynomial p(x) = 2x² + 5x + k, satisfying the relation, α² + β² + αβ = 21/4 then find the value of k. (2017 OD)
Solution:
Given polynomial is p(x) = 2x² + 5x + k
Here a = 2, b = 5, c = k

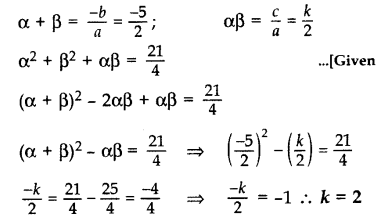
Question 35.
What must be subtracted from p(x) = 8x⁴ + 14x³ – 2x² + 8x – 12 so that 4x² + 3x – 2 is factor of p(x)? This question was given to group of students for working together. (2015)
Solution:

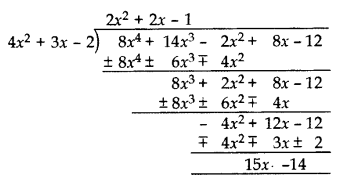
Polynomial to be subtracted by (15x – 14).

Question 36.
Find the values of a and b so that x⁴ + x³ + 8x² +ax – b is divisible by x² + 1. (2015)
Solution:

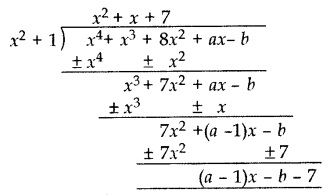
If x⁴ + x³ + 8x² + ax – b is divisible by x² + 1
Remainder = 0
(a – 1)x – b – 7 = 0
(a – 1)x + (-b – 7) = 0 . x + 0
a – 1 = 0, -b – 7 = 0
a = 1, b = -7
a = 1, b = -7

Question 37.
If a polynomial 3x⁴ – 4x³ – 16x² + 15x + 14 is divided by another polynomial x² – 4, the remainder comes out to be px + q. Find the value of p and q. (2014)
Solution:

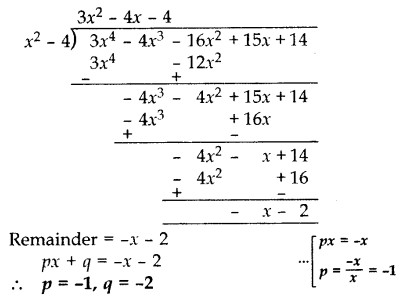
Question 38.
If the polynomial (x⁴ + 2x³ + 8x² + 12x + 18) is divided by another polynomial (x² + 5), the remainder comes out to be (px + q), find the values of p and q.
Solution:

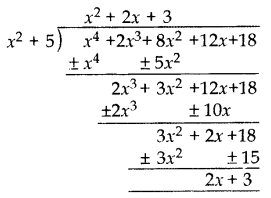
Remainder = 2x + 3
px + q = 2x + 3
p = 2 and q = 3.

CBSE Class 10 Maths Notes Chapter 2 Polynomials

• “Polynomial” comes from the word ‘Poly’ (Meaning Many) and ‘nomial’ (in this case meaning Term)-so it means many terms.
• A polynomial is made up of terms that are only added, subtracted or multiplied.
• A quadratic polynomial in x with real coefficients is of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0.
• Degree – The highest exponent of the variable in the polynomial is called the degree of polynomial. Example: 3x³ + 4, here degree = 3.
• Polynomials of degrees 1, 2 and 3 are called linear, quadratic and cubic polynomial respectively.
• A polynomial can have terms which have Constants like 3, -20, etc., Variables like x and y and Exponents like 2 in y².
• These can be combined using addition, subtraction and multiplication but NOT DIVISION.
• The zeroes of a polynomial p(x) are precisely the x-coordinates of the points, where the graph of y = p(x) intersects the x-axis.

Zeroes (α, β, γ) follow the rules of algebraic identities, i.e.,
(α + β)² = α² + β² + 2αβ
∴(α² + β²) = (α + β)² – 2αβ

DIVISION ALGORITHM:
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then
p(x) = g(x) × q(x) + r(x)
Dividend = Divisor x Quotient + Remainder

Remember this!

• If r (x) = 0, then g (x) is a factor of p (x).
• If r (x) ≠ 0, then we can subtract r (x) from p (x) and then the new polynomial formed is a factor of g(x) and q(x).

SabDekho

The Complete Educational Website

Bihar Board

UP Board

IAS Notes

Jac Board

MP Board

सम्पूर्ण व्याकरण

जीवनी

निबंध

टेन्स

सामान्य ज्ञान

Rajasthan Board