NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry
NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry Ex 9.1
Question 1.
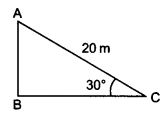
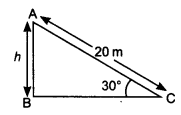
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see figure).
Solution:
Given: length of the rope (AC) = 20 m, ∠ACB = 30°
Let height of the pole (AB) = h metres
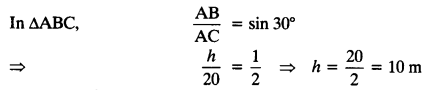
Hence, height of the pole = 10 m
Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
Let DB is a tree and AD is the broken part of it which touches the ground at C.
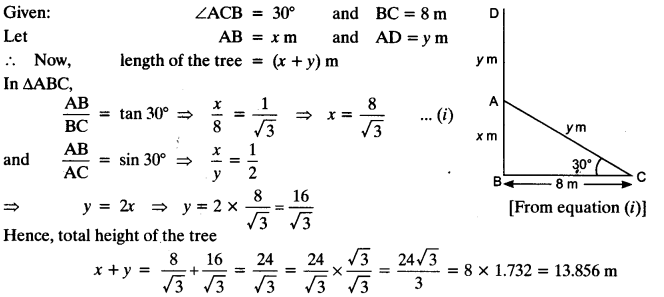
Question 3.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:
Let l1 is the length of slide for children below the age of 5 years and l2 is the length of the slide for elder children
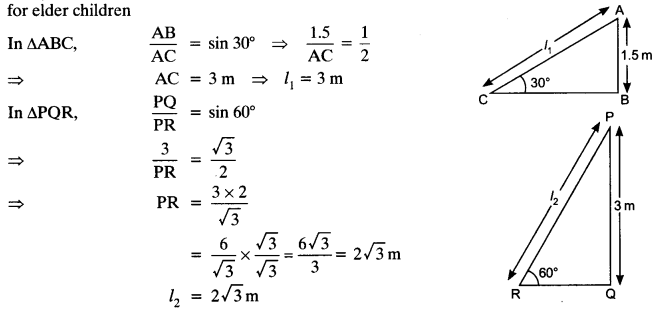
Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Solution:
Let h be the height of the tower
In ∆ABC,
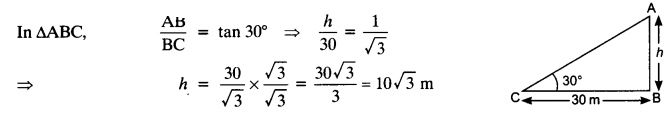
Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
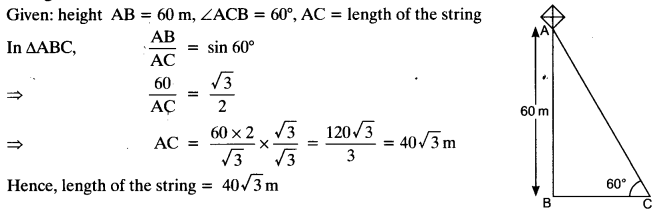
Question 6.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
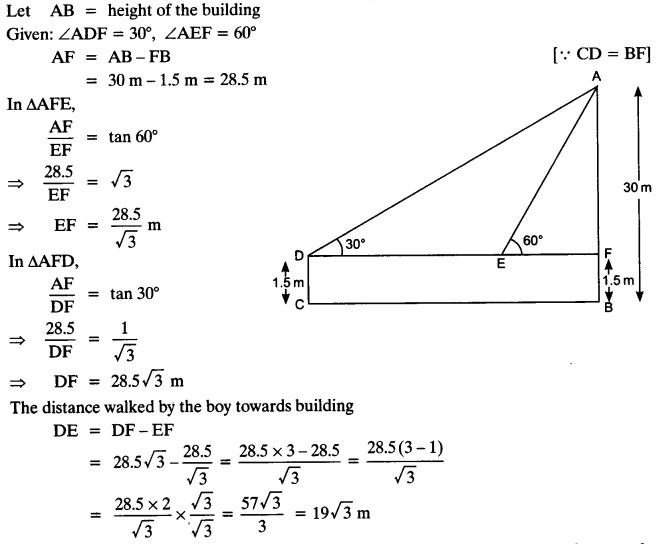
Question 7.
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:

Question 8.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:
Let the height of the pedestal AB = h m
Given: height of the statue = 1.6 m, ∠ACB = 45° and ∠DCB = 60°
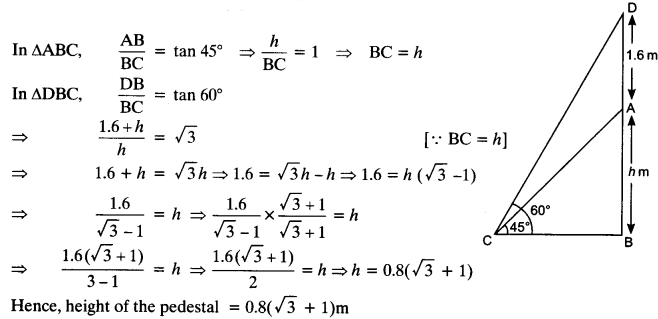
Question 9.
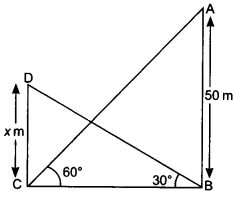
The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Given: height of the tower AB = 50 m,
∠ACB = 60°, ∠DBC = 30°
Let the height of the building CD = x m
In ∆ABC,
Question 10.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distance of the point from the poles.
Solution:

Question 11.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see the given figure). Find the height of the tower and the width of the CD and 20 m from pole AB.
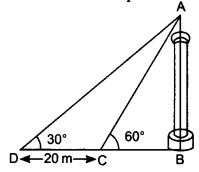
Solution:
Let the height of the tower AB = h m and BC be the width of the canal.

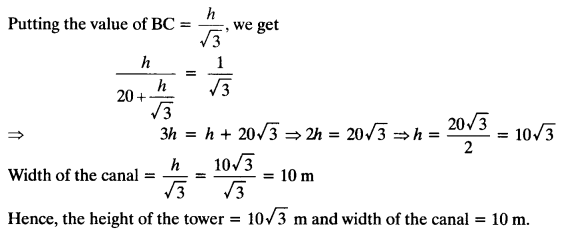
Question 12.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let height of the tower AB = (h + 7) m
Given: CD = 7 m (height of the building),
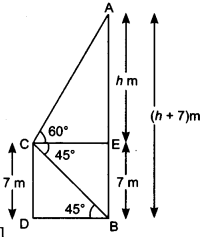

Question 13.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
Given: height of the lighthouse = 75 m
Let C and D are the positions of two ships.
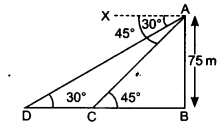
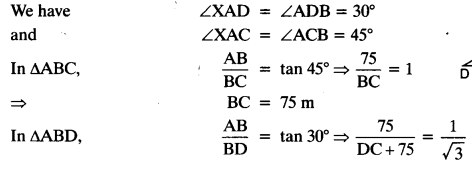
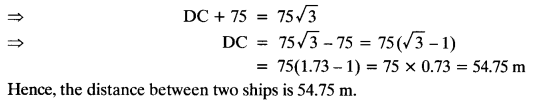
Question 14.
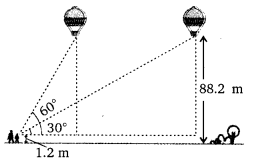
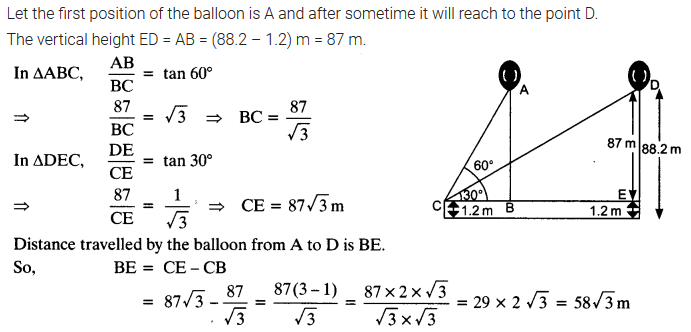
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30° (see figure). Find the distance travelled by the balloon during the interval.
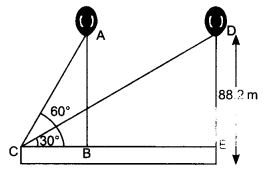
Solution:
Let the first position of the balloon is A and after sometime it will reach to the point D.
The vertical height ED = AB = (88.2 – 1.2) m = 87 m.
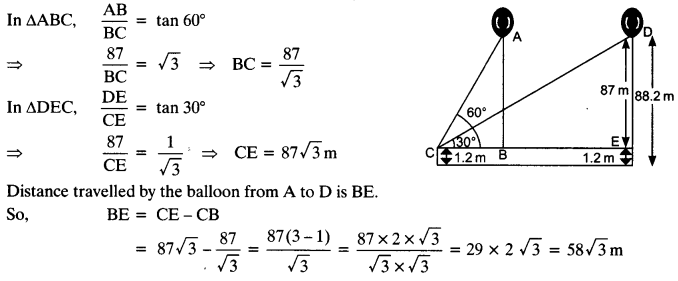
Question 15.
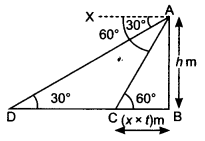
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:
Let the height of the tower AB = h m
Given: ∠XAD = ∠ADB = 30°
and ∠XAC = ∠ACB = 60°
Let the speed of the car = x m/sec
Distance CD = 6 x x = 6x m
Let the time taken from C to B = t sec.
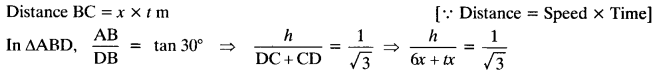
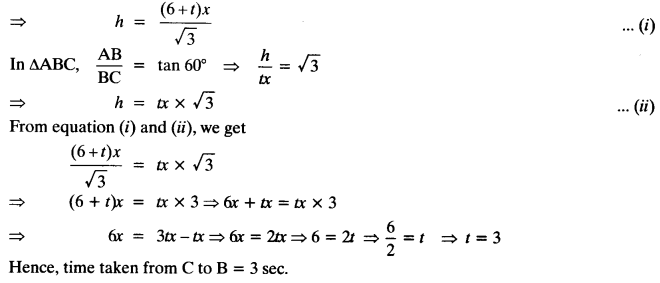
Question 16.
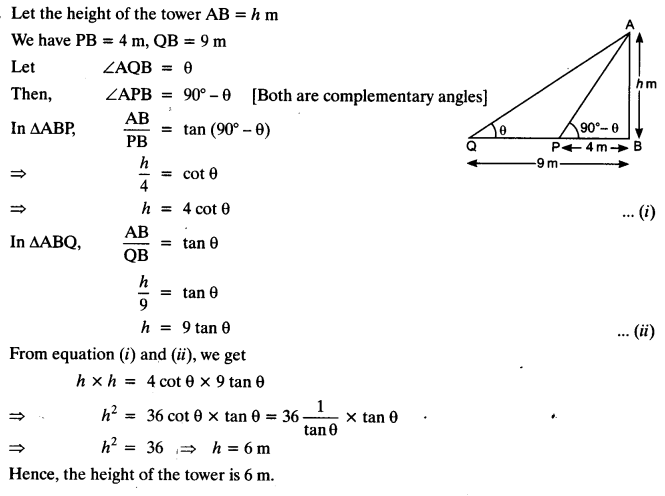
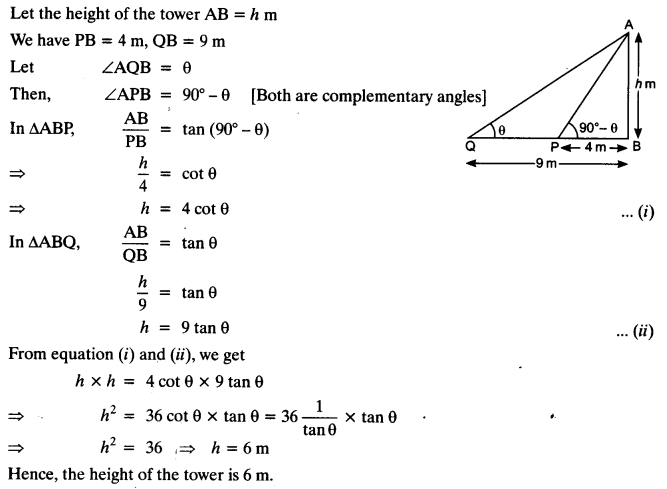
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
CBSE Class 10 Maths Notes Chapter 9 Some Applications of Trigonometry
Line of Sight
When an observer looks from a point E (eye) at an object O then the straight line EO between the eye E and the object O is called the line of sight.

Horizontal
When an observer looks from a point E (eye) to another point Q which is horizontal to E, then the straight line, EQ between E and Q is called the horizontal line.

Angle of Elevation
When the eye is below the object, then the observer has to look up from the point E to the object O. The measure of this rotation (angle θ) from the horizontal line is called the angle of elevation.

Angle of Depression
When the eye is above the object, then the observer has to look down from the point E to the object. The horizontal line is now parallel to the ground. The measure of this rotation (angle θ) from the horizontal line is called the angle of depression.

How to convert the above figure into the right triangle.
Case I: Angle of Elevation is known
Draw OX perpendicular to EQ.
Now ∠OXE = 90°
ΔOXE is a rt. Δ, where
OE = hypotenuse
OX = opposite side (Perpendicular)
EX = adjacent side (Base)

Case II: Angle of Depression is known
(i) Draw OQ’parallel to EQ
(ii) Draw perpendicular EX on OQ’.
(iii) Now ∠QEO = ∠EOX = Interior alternate angles
ΔEXO is an rt. Δ. where
EO = hypotenuse
OX = adjacent side (base)
EX = opposite side (Perpendicular)

- Choose a trigonometric ratio in such a way that it considers the known side and the side that you wish to calculate.
- The eye is always considered at ground level unless the problem specifically gives the height of the observer.
The object is always considered as a point.
Some People Have
Sin θ = Perpendicular/Hypotenuse
Curly Black Hair
Cos θ = Base/Hypotenuse
Turning Permanent Black.
Tan θ = Perpendicular/Base
NCERT Solutions For Class 10 Maths Chapter 9 Some Applications of Trigonometry Ex 9.1
Ex 9.1 Class 10 Maths Question 1.
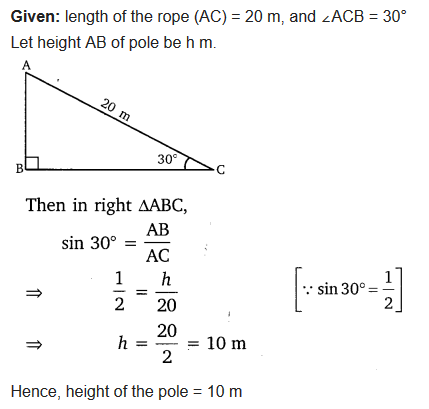
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Solution:
Ex 9.1 Class 10 Maths Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:

You can also download the free PDF of Ex 9.1 Class 10 Some Applications of Trigonometry NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Ex 9.1 Class 10 Maths Question 3.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:

Ex 9.1 Class 10 Maths Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Solution:
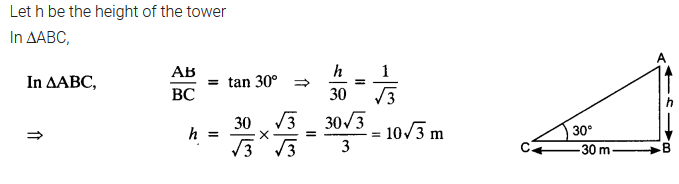
Ex 9.1 Class 10 Maths Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
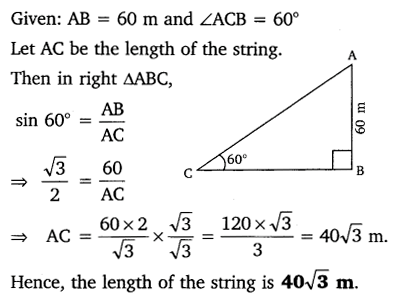
Ex 9.1 Class 10 Maths Question 6.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
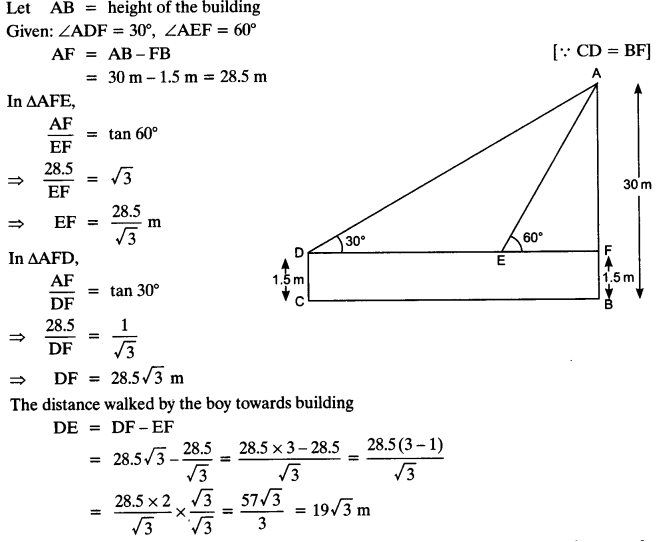
Ex 9.1 Class 10 Maths Question 7.
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:
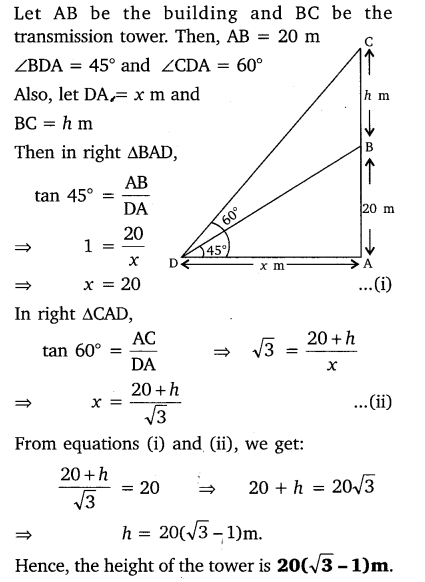
Ex 9.1 Class 10 Maths Question 8.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:

Ex 9.1 Class 10 Maths Question 9.
The angle of elevation of the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
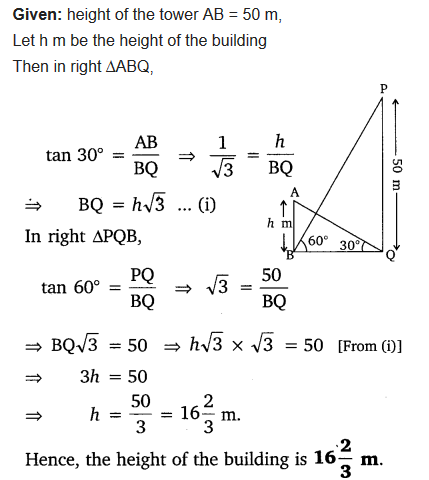
Ex 9.1 Class 10 Maths Question 10.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distance of the point from the poles.
Solution:

Ex 9.1 Class 10 Maths Question 11.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see the given figure). Find the height of the tower and the width of the CD and 20 m from pole AB.
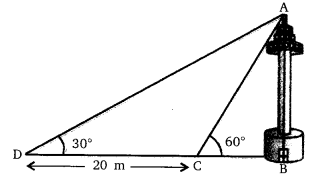
Solution:

Ex 9.1 Class 10 Maths Question 12.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
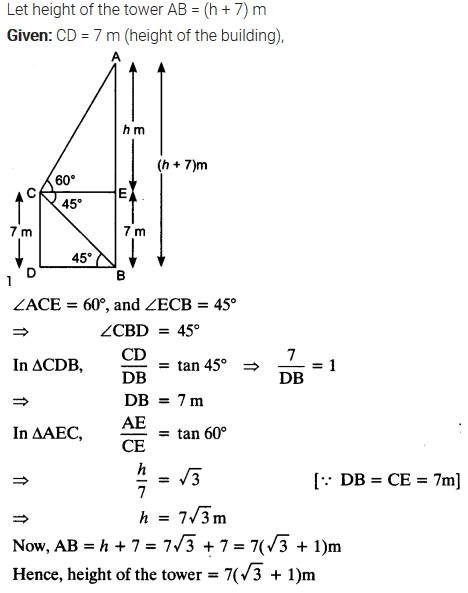
Ex 9.1 Class 10 Maths Question 13.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
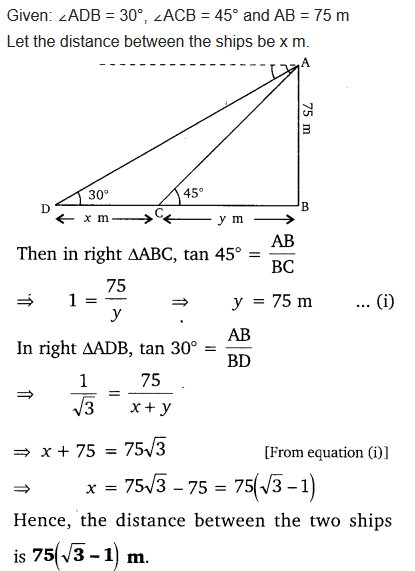
Ex 9.1 Class 10 Maths Question 14.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30° (see figure). Find the distance travelled by the balloon during the interval.
Solution:
Ex 9.1 Class 10 Maths Question 15.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:

Ex 9.1 Class 10 Maths Question 16.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Class 10 Maths Some Application Of Trigonometry Mind Maps
SOME APPLICATION OF TRIGONOMETRY
Introduction
The height or length of an object or the distance between two distinct objects can be determined with the help of trigonometric ratios.
Line of Sight and Angle of Elevation
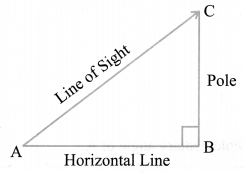
In the above figure, the line AC drawn from the eye of an observer at A to the top of the pole ‘C’ is called the line of sight. The observer is looking at the top of the pole. The angle BAC, so formed by the line of sight with the horizontal, is called the angle of elevation of the top of the pole from the eye of an observer.
Angle of Depression
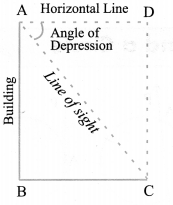
In the above figure, the line AC, is the line of sight as the observer is looking downwards from the top of the building at A towards the object at C. Here angle DAC, so formed by the line of sight with the horizontal, when the observer is lowering his/her head is called Angle of depression.
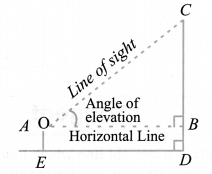
From the above figure, if we want to find the height CD of the pole without actually measuring it, we need the following information:
(i) Distance ED of the observer from the pole.
(ii) the angle of elevation ∠BAC, of the top of the pole.
(iii) the height AE of the observer if it is considerable.
Assuming that the above three conditions are known we can determine the height of the pole in the following way.
In the figure, CD = CB + BD. Here, BD = AE, which is the height of the observer.
To find BC, we will use trigonometric ratios of ∠BAC or ∠A.
In ∆ABC, the side BC is the opposite side to the known ∠A. Now we use either tan A or cot A, as these trigonometric ratios involve AB and BC to find BC.
Therefore, tan A = BC/AB or cot A = AB/BC, which on solving would give us BC. By adding AE to BC, you will get the height of the pole.
