NCERT Solutions for Class 9 Maths Chapter 10 Circles

NCERT Solutions for Class 9 Maths Chapter 10 Circles

NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.1

Ex 10.1 Class 9 Maths Question 1.
Fill in the blanks.
(i) The centre of a circle lies in ___ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ____ of the circle, (exterior/interior)

(iii) The longest chord of a circle is a ____ of the circle.

(iv) An arc is a ____ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and ____ of the circle.
(vi) A circle divides the plane, on which it lies, in ____ parts.
Solution:
(i) interior
(ii) exterior
(iii) diameter
(iv) semicircle
(v) the chord
(vi) three

Ex 10.1 Class 9 Maths Question 2.
Write True or False. Give reason for your answers.
(i) Line segment joining the centre to any point on the circle is a , radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution:
(i) True [∵ All points on the circle are equidistant from the centre]
(ii) False [ ∵ A circle can have an infinite number of equal chords]
(iii) False [∵ Each part will be less than a semicircle]
(iv) True [ ∵ Diameter = 2 x Radius]
(v) False [ ∵ The region between the chord and its corresponding arc is a segment]
(vi) True [ ∵ A circle is drawn on a plane]

NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2

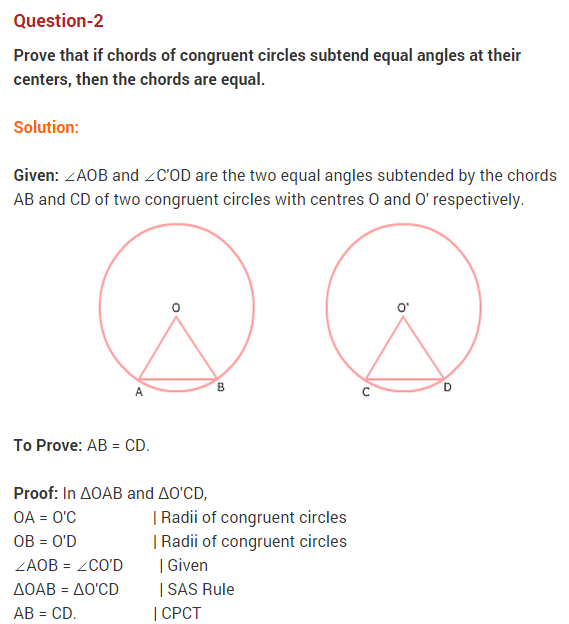
NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4

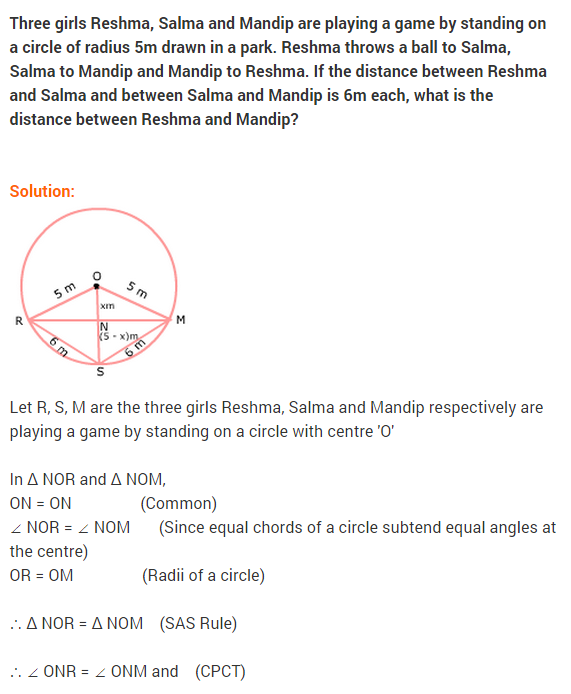
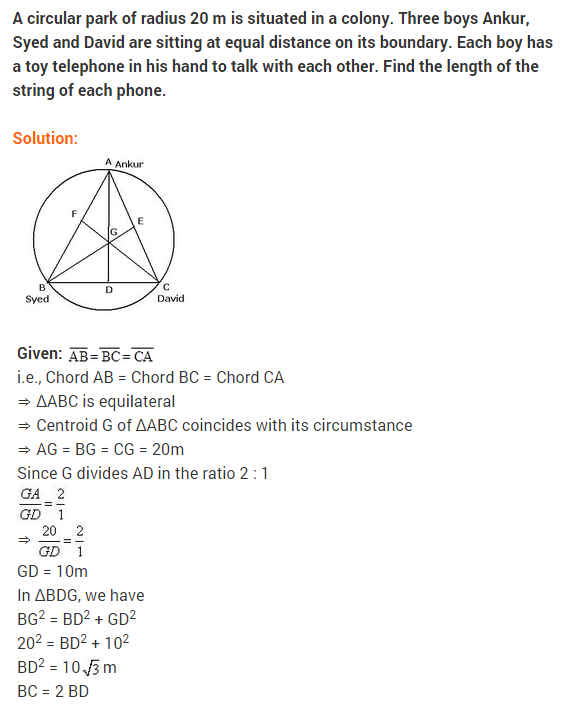
NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.5

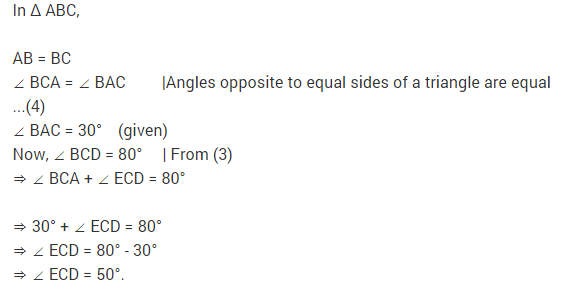
NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6

Ex 10.6 Class 9 Maths Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two circles with centres O and O’ which intersect each other at C and D.

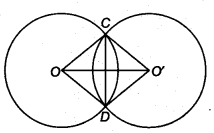
To prove: ∠OCO’ = ∠ODO’
Construction: Join OC, OD, O’C and O’D
Proof: In ∆ OCO’and ∆ODO’, we have
OC = OD (Radii of the same circle)
O’C = O’D (Radii of the same circle)
OO’ = OO’ (Common)
∴ By SSS criterion, we get
∆ OCO’ ≅ ∆ ODO’
Hence, ∠OCO’ = ∠ODO’ (By CPCT)

Ex 10.6 Class 9 Maths Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm, respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of the given circle and let its radius be cm.
Draw ON ⊥ AB and OM⊥ CD since, ON ⊥ AB, OM ⊥ CD and AB || CD, therefore points N, O, M are collinear.

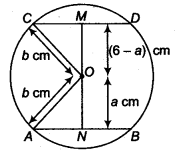
Let ON = a cm
∴ OM = (6 – a) cm
Join OA and OC.
Then, OA = OC = b c m
Since, the perpendicular from the centre to a chord of the circle bisects the chord.
Therefore, AN = NB= 2.5 cm and OM = MD = 5.5 cm
In ∆OAN and ∆OCM, we get
OA² = ON² + AN²
OC² = OM² + CM²
⇒ b² = a² + (2.5)²
and, b² = (6-a)² + (5.5)² …(i)
So, a² + (2.5)² = (6 – a)² + (5.5)²
⇒ a² + 6.25= 36-12a + a² + 30.25
⇒ 12a = 60
⇒ a = 5
On putting a = 5 in Eq. (i), we get
b² = (5)² + (2.5)²
= 25 + 6.25 = 31.25
So, r = √ 31.25 = 5.6cm (Approx.)

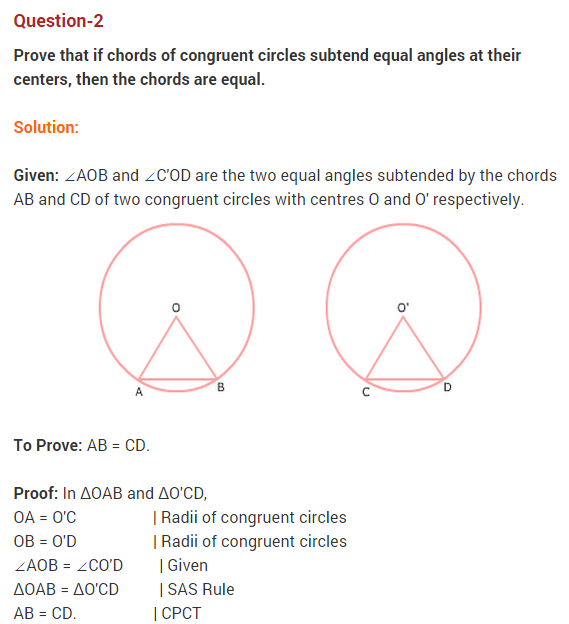
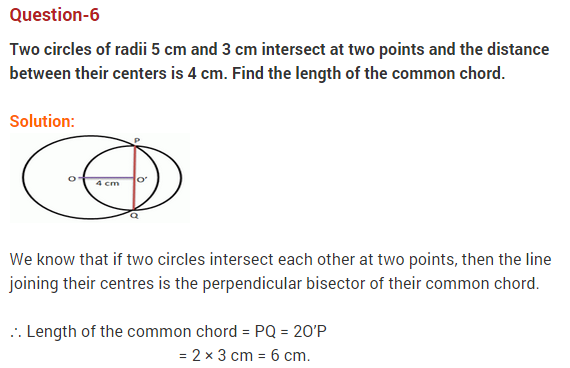
Ex 10.6 Class 9 Maths Question 3.
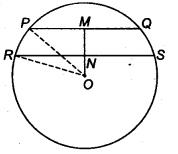
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre ?
Solution:
Let PQ and RS be two parallel chords of a circle with centre O such that PQ = 6 cm and RS = 8 cm.
Let a be the radius of circle.

Draw ON ⊥ RS, OM ⊥ PQ. Since, PQ || RS and ON ⊥ RS, OM⊥ PQ, therefore points 0,N,M are collinear.
∵ OM = 4 cm and M and N are the mid-points of PQ and RS respectively.
PM = MQ = 1/2 PQ = 6/2 = 3 cm
and RN = NS = 1/2 RS = 8/2 = 4 cm
In ∆OPM, we have
OP² = OM² + PM²
⇒ a² =4² + 3² = 16 + 9 = 25
⇒ a = 5
In ∆ORN, we have
⇒ OR² = ON² + RN²
⇒ a² = ON² + (4)²
⇒ 25 = ON² + 16
⇒ ON² = 9
⇒ ON = 3cm
Hence, the distance of the chord PS from the centre is 3 cm.

Ex 10.6 Class 9 Maths Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Since, an exterior angle of a triangle is equal to the sum of the interior opposite angles.

∴ In ∆BDC, we get
∠ADC = ∠DBC + ∠DCB …(i)
Since, angle at the centre is twice at a point on the remaining part of circle.
∴ ∠DCE = 1/2 ∠DOE
⇒ ∠DCB = 1/2 ∠DOE (∵ ∠DCE = ∠DCB)
∠ADC = 1/2 ∠AOC
∴ 1/2 ∠AOC = ∠ABC + 1/2 ∠DOE (∵ ∠DBC = ∠ABC)
∴ ∠ABC = 1/2 (∠AOC – ∠DOE)
Hence, ∠ABC is equal to half the difference of angles subtended by the chords AC and DE at the centre.

Ex 10.6 Class 9 Maths Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given: PQRS is a rhombus. PR and SQ are its two diagonals which bisect each other at right angles.
To prove: A circle drawn on PQ as diameter will pass through O.

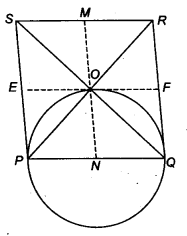
Construction: Through O, draw MN || PS and EF || PQ.
Proof : ∵ PQ = SR ⇒ 1/2 PQ = 1/2 SR
So, PN = SM
Similarly, PE = ON
So, PN = ON = NQ
Therefore, a circle drawn with N as centre and radius PN passes through P, O, Q.

Ex 10.6 Class 9 Maths Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
Since, ABCE is a cyclic quadrilateral, therefore

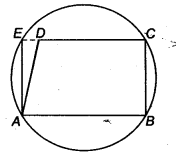
∠AED+ ∠ABC= 180°
(∵ Sum of opposite angle of a cyclic quadrilateral is 180°) .. .(i)
∵ ∠ADE + ∠ADC = 180° (EDC is a straight line)
So, ∠ADE + ∠ABC = 180°
(∵ ∠ADC = ∠ABC opposite angle of a || gm).. .(ii)
From Eqs. (i) and (ii), we get
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∴ In ∆AED We have
∠AED = ∠ADE
So, AD = AE
(∵ Sides opposite to equal angles of a triangle are equal)

Ex 10.6 Class 9 Maths Question 7.
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Solution:
(i) Let BD and AC be two chords of a circle bisect at P.

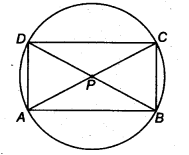
In ∆APB and ∆CPD, we get
PA = PC ( ∵ P is the mid-point of AC)
∠APB = ∠CPD (Vertically opposite angles)
and PB = PD (∵ P is the mid-point of BD)
∴ By SAS criterion
∆CPD ≅ ∆APB
∴ CD= AB (By CPCT) …(i)

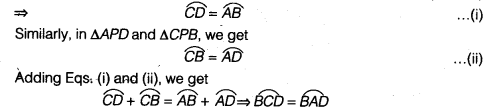
∴ BD divides the circle into two equal parts. So, BD is a diameter.
Similarly, AC is a diameter.
(ii) Now, BD and AC bisect each other.
So, ABCD is a parallelogram.
Also, AC = BD
∴ ABCD is a rectangle.

Ex 10.6 Class 9 Maths Question 8.
Bisectors of angles A, B and C of a ∆ABC intersect its circumcircle at D, E and F, respectively. Prove that the angles of the ∆DEF are 90° – 1/2 A, 90° – 1/2 B and 90° – 1/2 C.
Solution:
∵ ∠EDF = ∠EDA + ∠ADF
∵ ∠EDA and ∠EBA are the angles in the same segment of the circle.
∴ ∠EDA = ∠EBA
and similarly ∠ADF and ∠FCA are the angles in the same segment and hence

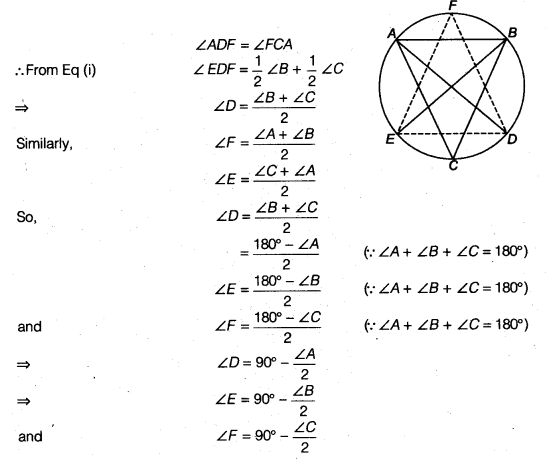
Ex 10.6 Class 9 Maths Question 9.
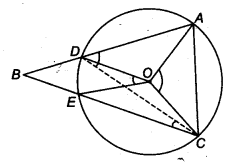
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Let O’ and O be the centres of two congruent circles.

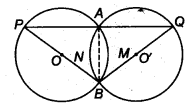
Since, AB is a common chord of these circles.
∴ ∠BPA = ∠BQA
(∵ Angle subtended by equal chords are equal)
⇒ BP = BQ

Ex 10.6 Class 9 Maths Question 10.
In any ∆ ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the ∆ABC.
Solution:
(i) Let bisector of ∠A meet the circumcircle of ∆ABC at M.
Join BM and CM.

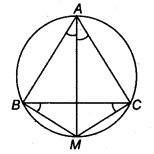
∴ ∠MBC = ∠MAC (Angles in same segment)
and ∠BCM = ∠BAM (Angles in same segment)
But ∠BAM = ∠CAM (∵ AM is bisector of ∠A)…. .(i)
∴ ∠MBC = ∠BCM
So, MB = MC (Sides opposite to equal angles are equal)
So, M must lie on the perpendicular bisector of BC
(ii) Let M be a point on the perpendicular bisector of BC which lies on circumcircle of ∆ ABC.
Join AM.

Since, M lies on perpendicular bisector of BC.
∴ BM = CM
∠MBC = ∠MCB
But ∠MBC = ∠MAC (Angles in same segment)
and ∠MCB = ∠BAM (Angles in same segment)
So, from Eq. (i),
∠BAM = ∠CAM
AM is the bisector of A.
Hence, bisector of ∠A and perpendicular bisector of BC at M which lies on circumcircle of ∆ABC.

Circles Class 9 Extra Questions Maths Chapter 10

Extra Questions for Class 9 Maths Chapter 10 Circles

IMPORTANT QUESTIONS

VERY SHORT ANSWER TYPE QUESTIONS
1. In the given figure, O is the centre of the circle with chords AP and BP being produced to R and Q respectively. If ∠QPR = 35°, find the measure of ∠AOB. [CBSE-14-17DIG1U]

Answer.

2. In the given figure, what is the measure of angle x ?

Answer. We know that exterior angle of a cyclic quadrilateral is equal to interior opposite angle.
.-. ∠CBE = ∠ADC
=> x = 120°

3. In the given figure, if O is the centre of circle and ∠POQ = 110°, then find ∠PRQ

Answer. We know that angle subtended by an arc at the centre is double the angle subtended by it at the remaining part of the circle.
∠PRQ =1/2 ∠POQ
= 1/2 x 110°
= 55°

4. In the given figure, ΔABC is an equilateral triangle and ABDC is a cyclic quadrilateral, then find the measure of ∠BDC.

Answer.

5. In the given figure, O is the centre of the circle. PQ is a chord of the circle and R is any point on the circle. If ∠PRQ = l and ∠OPQ = m, then find l + m.

Answer.

6. The given figure shows a circle with centre O in which a diameter AB bisects the chord PQ at the point R. If PR = RQ = 8 cm and RB = 4 cm, then find the radius of the circle.

Answer.

7. In the given figure, ABCD is a cyclic quadrilateral such that ∠ADB= 40° and ∠DCA = 70°, then find the measure of ∠DAB .

Answer.

8. In the figure, ‘O’ is the centre of the circle, ∠ABO= 20° and ∠ACO= 30°, where A, B, C are points on the circle. What is the value of x ?

Answer.

9. In the given figure, if O is the centre of circle. Chord AB is equal to radius of the circle, then find ∠ACB.

Answer.

10. In the given figure, if ∠OAB = 40°, then find the measure of ∠ACB. [NCERT Exemplar Problem]

Answer.

11. In the given figure, O is the centre of the circle. If∠BOC= 120°, then find the value of x.

Answer.

12. In the given figure, O is the centre of the circle, then compare the chords.

Answer. In chords AB and CD, AB is passing through the centre of the circle. AB is the diameter of circle. Thus, AB>CD [v diameter is the largest chord]

13. In the given figure, ∠ACP = 40° and ∠BPD = 120°, then find ∠CBD .

Answer.

14. In the given figure, if ∠SEC = 120°, ∠DCE = 25°, then find ∠BAC.

Answer.

15. AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, then find the distance of AB from the centre of the circle. [CBSE March 2012]

Answer.

16. In the given figure, if ∠DAB = 60°, ∠ABD= 50°, then find ∠ACB. [NCERT Exemplar Problem]

Answer.

17. In the given figure, AB || DC. If ∠A = 50°, then find the measure of ∠ABC. [NCERT Exemplar Problem]

Answer.

SHORT ANSWER QUESTIONS TYPE-I
18. Equal chords of a circle subtend equal angles at the centre. [CBSE March 2012]
Answer.

19. If the angles subtended by the chords of a circle at the centre are equal, then chords are equal. [CBSE March 2012]
Answer.

20. In the figure, O is the centre of the circle and ∠ABC= 45°. Show that OA⊥OC[/latex]. [CBSE March 2013]

Answer. Since angle subtended by an arc at the centre of the circle is double the angle subtended it at any point on the remaining part of the circle.

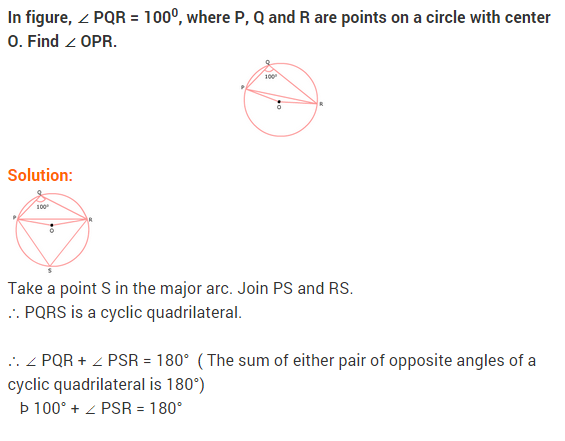
21. In the given figure, ∠PQR= 100°, where P,Q and R are points on a circle with centre O. Find ∠OPR. [CBSE March 2012]

Answer.

22. In figure, ABCD is a cyclic quadrilateral in which AB is extended till F and BE || DC. If ∠FBE= 20° and ∠DAB = 95°, then find∠ADC. [CBSE March 2012]

Answer.

23. In the figure, chord AB of circle with centre O, is produced to C such that BC = OB. CO is joined and produced to meet the circle in D. If ∠ACD = y and ∠AOD= x, show that x = 3y. [CBSE March 2011 ]

Answer.

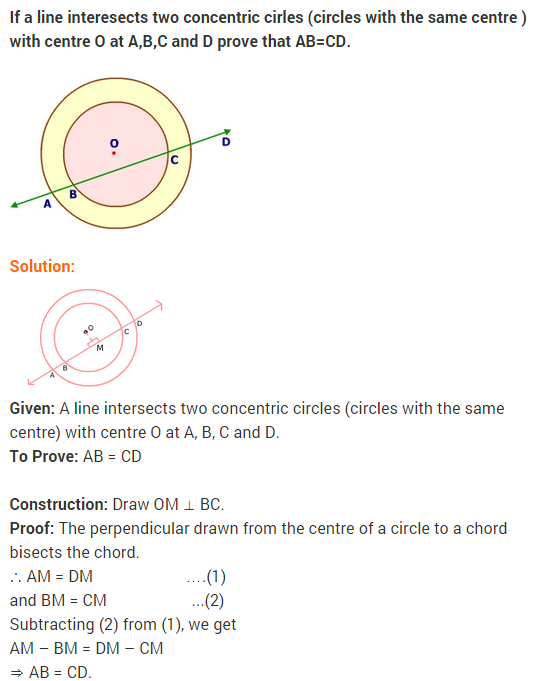
24. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see fig.). [CBSE March 2013]

Answer. Draw OM⊥ l
Since perpendicular from the centre of a circle to a chord of the circle bisects the chord.
BM = CM …(i)
and AM = DM …(ii)
Subtracting (i) from (ii), we have
AM – BM = DM – CM
AB = CD

25. In the given figure, P is the centre of the circle. Prove that : ∠ XPZ = 2(∠ XZY +∠  YXZ)

Answer.

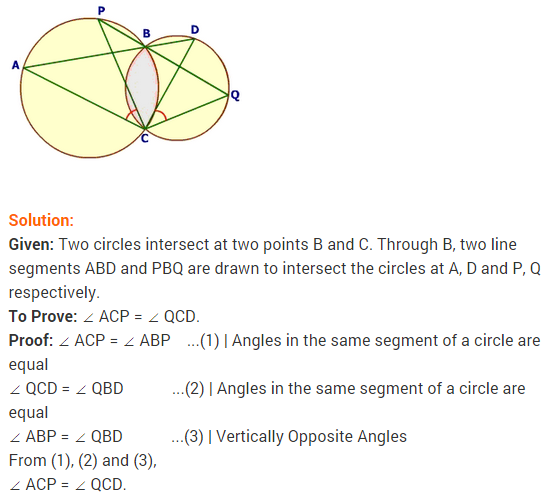
26. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see fig.). Prove that ∠ ACP =∠ QCD.

Answer.

27. If the diagonals of a cyclic quadrilateral are diameters of the circle through the opposite vertices of the quadrilateral. Prove that the quadrilateral is a rectangle. [CBSE-14-GDQNI3W]
Answer.

SHORT ANSWER QUESTIONS TYPE-II
28. If the non-parallel sides of a trapezium are equal, prove that it is cyclic. [CBSE March 2013]
Answer.

29. ABCD is a parallelogram. The circle through A, B and C intersects (produce if necessary) at E. Prove that AE = AD.
Answer.

30. ABCD is a cyclic quadrilateral in which AB and CD when produced meet in E and EA = ED. Prove that : (i) AD\\BC (ii) EB = EC
Answer.

31. If two equal chords of a circle intersect within a circle, prove that the line segment joining the point of intersection to the centre makes equal angles with the chords. [CBSE-15-NS72LP7]
Answer.

32. Two circles whose centres are O and O’ intersect at P. Through P, a line parallel to OO’, intersecting the circles at C and D is drawn as shown in the figure. Prove the CD = 200′. [CBSE-15-6DWMW5A] [CBSE-14-ERFKZ8H]

Answer.

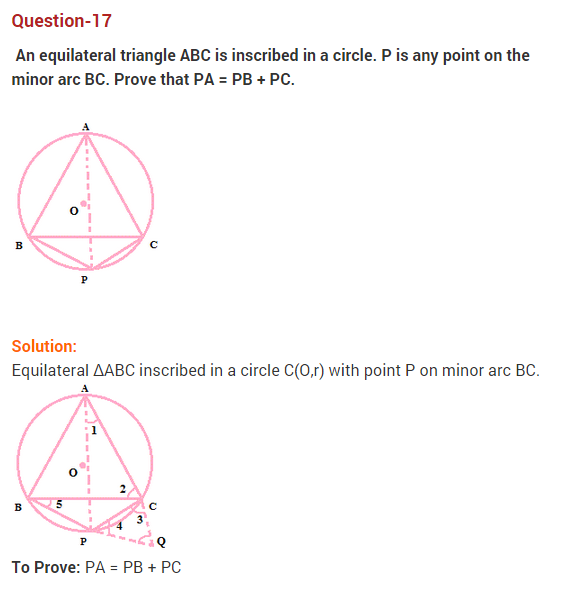
33. If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC . [NCERT Exemplar Problem]
Answer.

34. In the given figure, AB and CD are two equal chords of a circle with centre O. OP and OQ are perpendiculars on chords AB and CD respectively. If ∠ POQ  = 120°, find ∠APQ . [CBSE-14-ERFKZ8H]

Answer.

LONG ANSWER TYPE QUESTIONS
35. Show that the quadrilateral formed by angle bisectors of a cyclic quadrilateral, is also cyclic. [CBSE March 2012]

Answer.

36. Prove that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. [CBSE March 2012]
Answer.

37. Prove that the angle bisectors of the angle formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right angle.
Answer.

38. Bisectors of angles A, B and C of triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the ΔDEF are 90° -∠ A/2 ,90° – ∠ B/2 and 90°- ∠ C/2 respectively.
Answer.

39. In the given figure, O is the centre of a circle of radius r cm, OP and OQ are perpendiculars to AB and CD respectively and PQ = 1 cm. If AB II CD, AB = 6cm and CD = 8cm, determiner. [ CBSE-15-6DWMW5A]

Answer. Since the perpendicular drawn from the centre of the circle to a chord bisects the chord. Therefore, P and Q are mid-points of AB and CD respectively.

40. If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see fig.), prove that arc CXA + arc DZB = arc AYD + arc BWC = semicircle. [NCERT Exemplar Problem]

Answer. Given two chords AB and CD of a circle intersect at right angle. Let P be the point of intersection of the chord and O be the centre of circle AYDZBWCX.

41. In the given figure, AC is a diameter of the circle with centre O. Chord BD is perpendicular to AC. Write down the measures of angles a, b, c and d in terms of x. [CBSE-15-NS72LP7]

Answer.

42. The bisector of ∠B of an isosceles triangle ABC with AB = AC meets the circumcircle of ΔABC at P as shown in the given figure. If AP and BC produced meet at Q, prove that CQ = CA. [CBSE-14-GDQNI3W]

Answer.

Value Based Questions
1. A small cottage industry employing people from a nearby slum area prepares round table cloths having six equal designs in the six segment formed by equal chords AB, BC, CD, DE, EF and FA. If O is the centre of round table cloth (see figure). Find ∠AOB, ∠AEB and ∠AFB.What value is depicted through this question ? [CBSE-14-17DJG1U]

Answer.

Value depicted : By employing people from a slum area to prepare round table cloths realize their social responsibility to work for helping the ones in need.

2. Three students Priyanka, Sania and David are protesting against killing innocent animals for commercial purposes in a circular park of radius 20 m. They are standing at equal distances on its boundary by holding banners in their hands.
(i) Find the distance between each of them.
(ii) Which mathematical concept is used in it ?
(iii) How does an act like this reflects their attitude towards society ?
Answer.

3. A circular park of radius 10 m is situated in a colony. Three students Ashok, Raman and Kanaihya are standing at equal distances on its circumference each having a toy telephone in his hands to talk each other about Honesty, Peace and Discipline.
(i) Find the length of the string of each phone.
(ii) Write the role of discipline in students’ life.
Answer. Let us assume, A, B and C be the position of three students Ashok, Raman and Kanaihya respectively on the circumference of the circular park with centre O and radius 10 m. Since the centre of circle coincides with the centroid of the equilateral ΔABC.

4. Three scouts Rajat, Rohit and Ramit in the cultural show holded three stringed balloons with a message ‘Stop Child Labour’. Keeping themselves on the boundary of a circle of radius 25 cm, each scout holded the string tightly. Find the distance between Rajat and Ramit, when distance between Rajat and Rohit and Rohit and Ramit is 30 cm. What message was given by scouts and why ?
Answer.