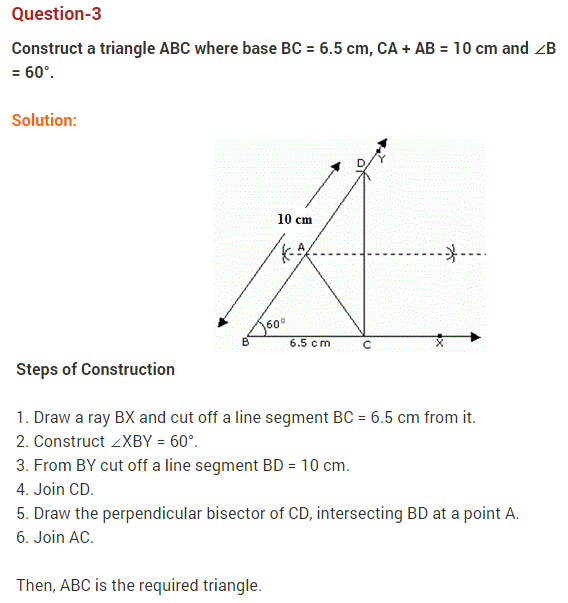
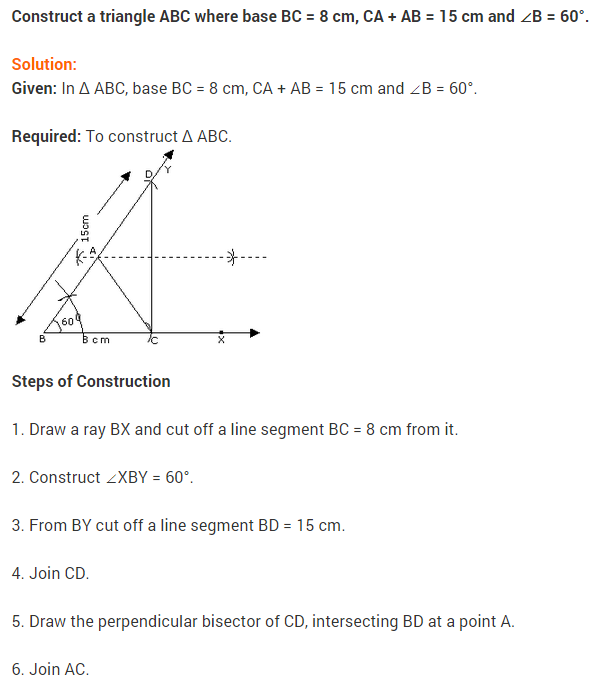
NCERT Solutions for Class 9 Maths Chapter 11 Constructions

NCERT Solutions for Class 9 Maths Chapter 11 Constructions

NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1

Ex 11.1 Class 9 Maths Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steprf of Construction:
Step I : Draw AB¯¯¯¯¯¯¯¯.
Step II : Taking O as centre and having a suitable radius, draw a semicircle, which cuts OA¯¯¯¯¯¯¯¯ at B.
Step III : Keeping the radius same, divide the semicircle into three equal parts such that BC˘=CD˘=DE˘ .
Step IV : Draw OC¯¯¯¯¯¯¯¯ and OD¯¯¯¯¯¯¯¯.
Step V : Draw OF¯¯¯¯¯¯¯¯, the bisector of ∠COD.

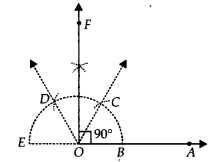
Thus, ∠AOF = 90°
Justification:
∵ O is the centre of the semicircle and it is divided into 3 equal parts.
∴ \breve { BC } =\quad \breve { CD } \quad =\quad \breve { DE }

BC˘=CD˘=DE˘
⇒ ∠BOC = ∠COD = ∠DOE [Equal chords subtend equal angles at the centre]
And, ∠BOC + ∠COD + ∠DOE = 180°
⇒ ∠BOC + ∠BOC + ∠BOC = 180°
⇒ 3∠BOC = 180°
⇒ ∠BOC = 60°
Similarly, ∠COD = 60° and ∠DOE = 60°
∵ OF¯¯¯¯¯¯¯¯ is the bisector of ∠COD
∴ ∠COF = 1/2 ∠COD = 1/2 (60°) = 30°
Now, ∠BOC + ∠COF = 60° + 30°
⇒ ∠BOF = 90° or ∠AOF = 90°

Ex 11.1 Class 9 Maths Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of Construction:
Stept I : Draw OA¯¯¯¯¯¯¯¯.
Step II : Taking O as centre and with a suitable radius, draw a semicircle such that it intersects OA¯¯¯¯¯¯¯¯. at B.
Step III : Taking B as centre and keeping the same radius, cut the semicircle at C. Now, taking C as centre and keeping the same radius, cut the semicircle at D and similarly, cut at E, such that BC˘=CD˘=DE˘
Step IV : Draw OC¯¯¯¯¯¯¯¯ and OD¯¯¯¯¯¯¯¯.
Step V : Draw OF¯¯¯¯¯¯¯¯, the angle bisector of ∠BOC.
Step VI : Draw OG¯¯¯¯¯¯¯¯, the ajngle bisector of ∠FOC.

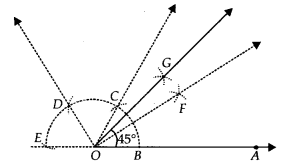
Thus, ∠BOG = 45° or ∠AOG = 45°
Justification:
∵ BC˘=CD˘=DE˘
∴ ∠BOC = ∠COD = ∠DOE [Equal chords subtend equal angles at the centre]
Since, ∠BOC + ∠COD + ∠DOE = 180°
⇒ ∠BOC = 60°
∵ OF¯¯¯¯¯¯¯¯ is the bisector of ∠BOC.
∴ ∠COF = 1/2 ∠BOC = 1/2(60°) = 30° …(1)
Also, OG¯¯¯¯¯¯¯¯ is the bisector of ∠COF.
∠FOG = 1/2∠COF = 1/2(30°) = 15° …(2)
Adding (1) and (2), we get
∠COF + ∠FOG = 30° + 15° = 45°
⇒ ∠BOF + ∠FOG = 45° [∵ ∠COF = ∠BOF]
⇒ ∠BOG = 45°

Ex 11.1 Class 9 Maths Question 3.
Construct the angles of the following measurements
(i) 30°
(ii) 22 1/2∘
(iii) 15°
Solution:
(i) Angle of 30°
Steps of Construction:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : With O as centre and having a suitable radius, draw an arc cutting OA¯¯¯¯¯¯¯¯ at B.
Step III : With centre at B and keeping the same radius as above, draw an arc to cut the previous arc at C.
Step IV : Join OC¯¯¯¯¯¯¯¯ which gives ∠BOC = 60°.
Step V : Draw OD¯¯¯¯¯¯¯¯, bisector of ∠BOC, such that ∠BOD = 1/2∠BOC = 1/2(60°) = 30°

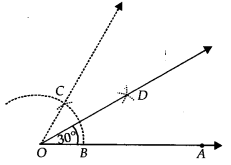
Thus, ∠BOD = 30° or ∠AOD = 30°

(ii) Angle of 22 1/2∘
Steps of Construction:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : Construct ∠AOB = 90°
Step III : Draw OC¯¯¯¯¯¯¯¯, the bisector of ∠AOB, such that
∠AOC = 1/2∠AOB = 1/2(90°) = 45°
Step IV : Now, draw OD, the bisector of ∠AOC, such that
∠AOD = 1/2∠AOC = 1/2(45°) = 22 1/2∘

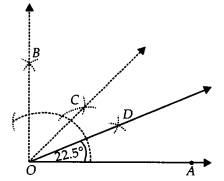
Thus, ∠AOD = 22 1/2∘

(iii) Angle of 15°
Steps of Construction:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : Construct ∠AOB = 60°.
Step III : Draw OC, the bisector of ∠AOB, such that
∠AOC = 1/2∠AOB = 1/2(60°) = 30°
i.e., ∠AOC = 30°
Step IV : Draw OD, the bisector of ∠AOC such that
∠AOD = 1/2∠AOC = 1/2(30°) = 15°

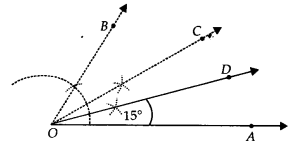
Thus, ∠AOD = 15°

Ex 11.1 Class 9 Maths Question 4.
Construct the following angles and verify by measuring them by a protractor
(i) 75°
(ii) 105°
(iii) 135°
Solution:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : With O as centre and having a suitable radius, draw an arc which cuts OA¯¯¯¯¯¯¯¯ at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc of step II.
Step V : Join OC¯¯¯¯¯¯¯¯ and OD¯¯¯¯¯¯¯¯, which gives ∠COD = 60° = ∠BOC.
Step VI : Draw OP¯¯¯¯¯¯¯¯, the bisector of ∠COD, such that
∠COP = 1/2∠COD = 1/2(60°) = 30°.
Step VII: Draw OQ¯¯¯¯¯¯¯¯, the bisector of ∠COP, such that
∠COQ = 1/2∠COP = 1/2(30°) = 15°.

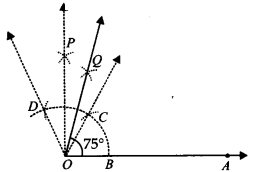
Thus, ∠BOQ = 60° + 15° = 75°∠AOQ = 75°

(ii) Steps of Construction:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : With centre O and having a suitable radius, draw an arc which cuts OA¯¯¯¯¯¯¯¯ at B.
Step III : With centre B and keeping the same radius, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc drawn in step II.
Step V : Draw OP, the bisector of CD which cuts CD at E such that ∠BOP = 90°.
Step VI : Draw OQ¯¯¯¯¯¯¯¯, the bisector of BC˘ such that ∠POQ = 15°

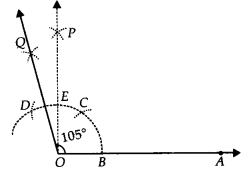
Thus, ∠AOQ = 90° + 15° = 105°

(iii) Steps of Construction:
Step I : Draw OP¯¯¯¯¯¯¯¯.
Step II : With centre O and having a suitable radius, draw an arc which cuts OP¯¯¯¯¯¯¯¯ at A
Step III : Keeping the same radius and starting from A, mark points Q, R and S on the arc of step II such that AQ˘=QR˘=RS˘ .
StepIV :Draw OL¯¯¯¯¯¯¯, thebisector of RS˘ which cuts the arc RS˘ at T.
Step V : Draw OM¯¯¯¯¯¯¯¯¯, the bisector of RT˘.

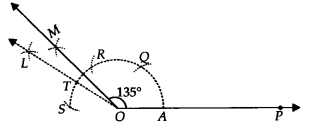
Thus, ∠POQ = 135°

Ex 11.1 Class 9 Maths Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
pt us construct an equilateral triangle, each of whose side = 3 cm(say).
Steps of Construction:
Step I : Draw OA¯¯¯¯¯¯¯¯.
Step II : Taking O as centre and radius equal to 3 cm, draw an arc to cut OA¯¯¯¯¯¯¯¯ at B such that OB = 3 cm
Step III : Taking B as centre and radius equal to OB, draw an arc to intersect the previous arc at C.
Step IV : Join OC and BC.

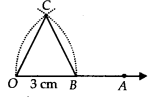
Thus, ∆OBC is the required equilateral triangle.

Justification:
∵ The arcs OC˘ and BC˘ are drawn with the same radius.
∴ OC˘ = BC˘
⇒ OC = BC [Chords corresponding to equal arcs are equal]
∵ OC = OB = BC
∴ OBC is an equilateral triangle.

NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.2

Constructions Class 9 Extra Questions Maths Chapter 11

Extra Questions for Class 9 Maths Chapter 11 Constructions

IMPORTANT QUESTIONS

VERY SHORT ANSWER TYPE QUESTIONS
1. Construct an angle of 90° at the initial point of the given ray. [CBSE-15-6DWMW5A]
Answer.

2. Draw a line segment PQ = 8.4 cm. Divide PQ into four equal parts using ruler and compass. [CBSE-14-ERFKZ8H], [CBSE – 14-GDQNI3W], [CBSE-14-17DIG1U]
Answer. Steps of construction :

1. Draw a line segment PQ = 8.4 cm.
2. With P and Q as centres, draw arcs of radius little more than half of PQ. Let his line intersects PQ in M.
3. With M and Q as centres, draw arcs of radius little more than half of MQ. Let this line intersects PQ in N.
4. With P and M as centres, draw arcs of radius little more than half of PM. Let this line intersects PQ in L. Thus, L, M and N divide the line segment PQ in four equal parts.
   

3. Draw any reflex angle. Bisect it using compass. Name the angles so obtained. [CBSE-15-NS72LP7]
Answer.

4. Why we cannot construct a ΔABC, if ∠A=60°, AB — 6 cm, AC + BC = 5 cm but construction of A ABC is possible if ∠A=60°, AB = 6 cm and AC – BC = 5 cm. [CBSE-14-GDQNI3W]
Answer. We know that, by triangle inequality property, construction of triangle is possible if sum of two sides of a triangle is greater than the third side.
Here, AC + BC = 5 cm which is less than AB ( 6 cm)
Thus, ΔABC is not possible.
Also, by triangle inequality property, construction of triangle is possible, if difference of two
sides of a triangle is less than the third side
Here, AC – BC = 5 cm, which is less than AB (6 cm)
Thus, ΔABC is possible.

5. Construct angle of [52 1/2]0 using compass only. [CBSE-14-17DIG1U]
Answer.

SHORT ANSWER QUESTIONS TYPE-I
6. Using ruler and compass, construct 4∠XYZ, if ∠XYZ= 20° [CBSE-14-ERFKZ8H]
Answer.

7. Construct an equilateral triangle LMN, one of whose side is 5 cm. Bisect ∠ M of the triangle. [CBSE March 2012]
Answer. Steps of construction :

1.  Draw a line segment LM = 5 cm.
2. Taking L as centre and radius 5 cm draw an arc.
3. Taking M as centre and radius draw an other arc intersecting previous arc at N.
4. Join LN and MN. Thus, ΔLMN is the required equilateral triangle.
5. Taking M as centre and any suitable radius, draw an arc intersecting LM at P and MN at Q.
6. Taking P and Q as centres and same radii, draw arcs intersecting at S.
7. Join MS and produce it meet LN at R. Thus, MSR is the required bisector of ∠M.
   

SHORT ANSWER QUESTIONS TYPE-II
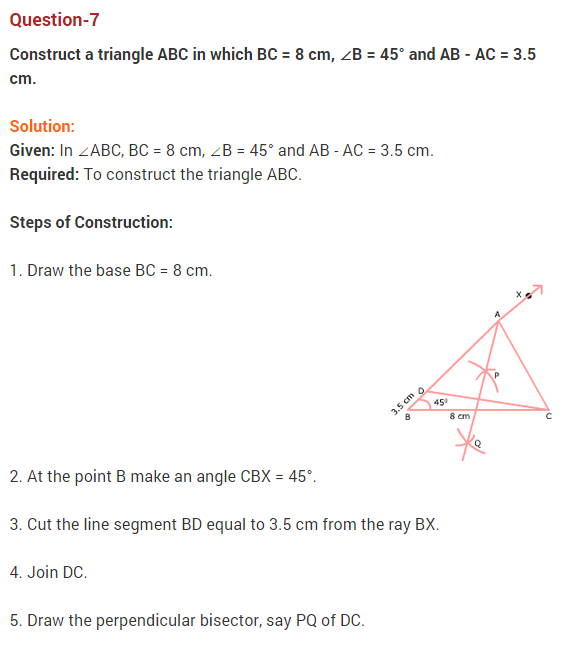
8. Construct a A ABC with BC = 8 cm, ∠B= 45° and AB – AC = 3.1 cm. [CBSE-15-NS72LP7]
Answer.

9. Construct an isosceles triangle whose two equal sides measure 6 cm each and whose base is 5 cm. Draw the perpendicular bisector of its base and show that it passes through the opposite vertex [CBSE-15-6DWMW5A]
Answer. Steps of construction :

1. Draw a line segment AB = 5 cm.
2. With A and B as centres, draw two arcs of radius 6 cm and let they intersect each other in C.
3.  Join AC and BC to get ΔABC.
4. With A and B as centres, draw two arcs of radius little more than half of AB. Let they intersect each other in P and Q. Join PQ and produce, to pass through C.
   

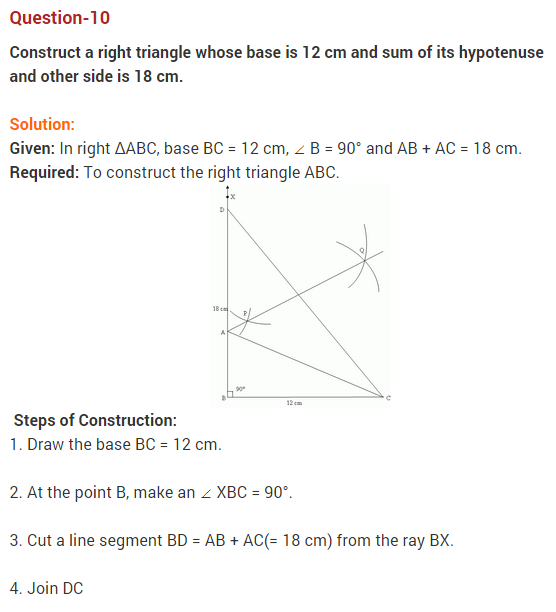
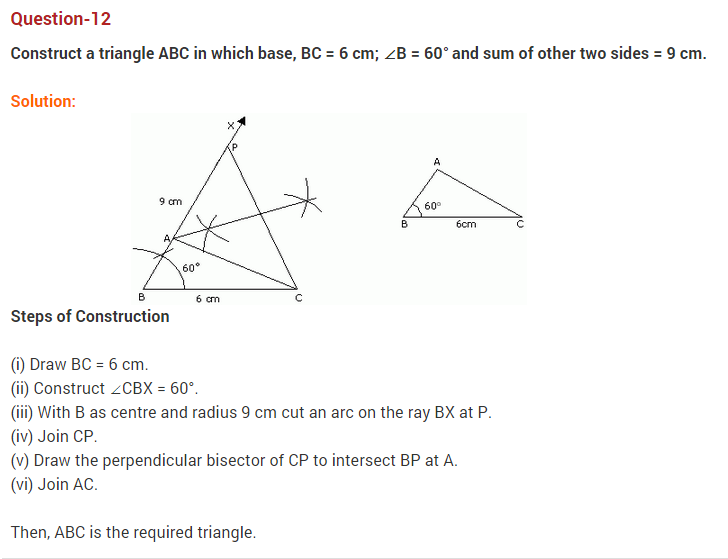
10. Construct a right triangle whose base is 8 cm and sum of the hypotenuse and other side is 16 cm.
Answer. Given : In ΔABC, BC = 8 cm, ∠B= 90° and AB + AC = 16 cm.
Required : To construct ΔABC.
Steps of construction:

1. Draw a line segment BC = 8 cm.
2. At B, Draw ∠CBX = 90°.
3. From ray BX, cut off BE = 16 cm.
4.  Join CE .
5. Draw the perpendicular bisector of EC meeting BE at A.
6. Join AC to obtain the required ΔABC.
   

11. To construct an isosceles ΔABC in which base BC = 4 cm, sum of the perpendicular from A to BC and side AB = 6.5 cm.
Answer. Given : In  ΔABC, BC = 4 cm and sum of the perpendicular from A to BC and side AB = 6.5 cm.
Required : To construct ΔABC.
Steps of construction :

1. Draw any line segment BC = 4 cm.
2. Draw ‘p’ the perpendicular bisector of BC and let it intersect BC in R
3. Cut off PQ = 6.5 cm.
4. Join QB.
5. Draw the perpendicular bisector of BQ and let it intersect PQ in A.
6. Join AB and AC. Thus, ΔABC is the required triangle.
   

12. Construct an  equilateral triangle of altitude 6 cm. [CBSE-15-6DWMW5A]
Answer. Steps of construction :

1. Draw any line l.
2. Take any point M on it and draw  a line p perpendicular to l.
3. With M as centre, cut off MC = 6 cm
4. At C, with initial line CM construct angles of measures 30° on both sides and let these lines intersect line l in A and B. Thus, ΔABC is the required triangle.
   

13. Draw a line segment QR = 5 cm. Construct perpendiculars at point Q and R to it. Name them as QX and RY respectively. Are they both parallel ? [CBSE-15-NS72LP7] [CBSE-14-ERFKZ8H]
Answer. Steps of construction :

1. Draw a line segment QR = 5 cm.
2. With Q as centre, construct an angle of 90° and let this line through Q is QX.
3. With R as centre, construct an angle of 90° and let this line through R is RY. Yes, the perpendicular lines QX and- RY are parallel.
   

LONG ANSWER TYPE QUESTIONS
14. Construct a triangle ABC in which BC = 4.7 cm, AB + AC = 8.2 cm and ∠C = 60°. [CBSE March 2012]
Answer. Given : In ΔABC, BC= 4.7 cm, AB + AC = 8.2 cm and ∠C= 60°.
Required : To construct ΔABC.

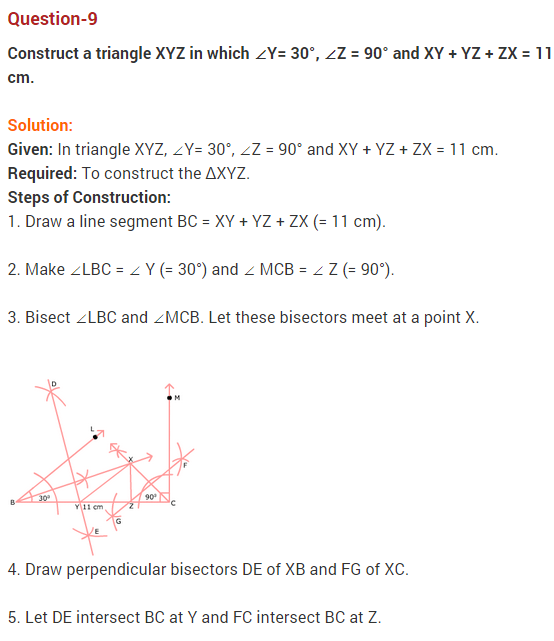
15. To construct a triangle, given its perimeter and its two base angles, e.g., construct a triangle with perimeter 10 cm and base angles 60° and 45°. [CBSE March 2012]
Answer.

16. Construct ΔXYZ, if its perimeter is 14 cm, one side of length 5 cm and ∠X= 45°. [CBSE-14-ERFKZ8H]
Answer. Here, perimeter of ΔXYZ = 14 cm and one side XY = 5 cm
.-. YZ + XZ = 14 – 5 = 9 cm and ∠X = 45°.
Steps of construction :

1. Draw a line segment XY = 5 cm.
2. Construct an ∠YXA = 45° with the help of compass and ruler.
3. From ray XA, cut off XB – 9 cm.
4. Join BY.
5. Draw perpendicular bisector of BY and let it intersect XB in Z.
6. Join ZY. Thus, ΔXYZ is the required triangle.