NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Ex 12.1
Ex 12.1 Class 9 Maths Question 1.
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side a. Find the area of the signal board, using Heron’s formula.If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
Let each side of the equilateral triangle be a.
Semi-perimeter of the triangle,
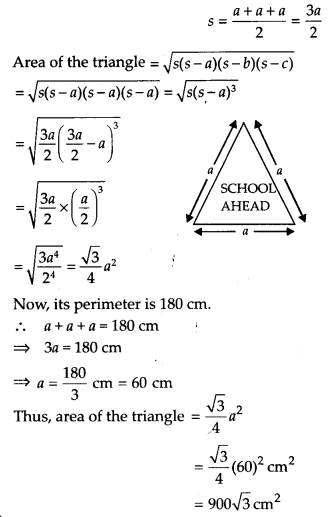
Ex 12.1 Class 9 Maths Question 2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?
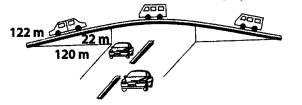
Solution:
Let the sides of the triangular will be
a = 122m, b = 12cm, c = 22m
Semi-perimeter, s = a+b+c/2
(122+120+22/4)m = 264/2 m = 132m
The area of the triangular side wall
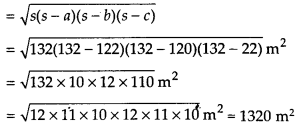
Rent for 1 year (i.e. 12 months) per m2 = Rs. 5000
∴ Rent for 3 months per m2 = Rs. 5000 x 3/12
= Rent for 3 months for 1320 m2 = Rs. 5000 x 3/12 x 1320 = Rs. 16,50,000.
Ex 12.1 Class 9 Maths Question 3.
There is a slide in a park. One of its side Company hired one of its walls for 3 months.walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see figure). If the sides of the wall are 15 m, 11 m and 6m, find the area painted in colour.
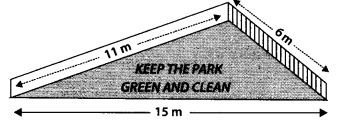
Solution:
Let the sides of the wall be
a = 15m, b = 11m, c = 6m
Semi-perimeter,

Thus, the required area painted in colour
= 20√2 m2
Ex 12.1 Class 9 Maths Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Let the sides of the triangle be a =18 cm, b = 10 cm and c = x cm
Since, perimeter of the triangle = 42 cm
∴ 18cm + 10 cm + xcm = 42
x = [42 – (18 + 10)cm = 14cm
Now, semi-permimeter, s = 42/2cm = 21 cm
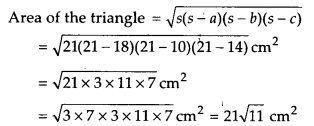
Thus, the required area of the triangle = 21√11 cm2
Ex 12.1 Class 9 Maths Question 5.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Let the sides of the triangle be
a = 12x cm, b = 17x cm, c = 25x cm
Perimeter of the triangle = 540 cm
Now, 12x + 17x + 25x = 540
⇒ 54x = 54 ⇒ x = 10
∴ a = (12 x10)cm = 120cm,
b = (17 x 10) cm = 170 cm
and c = (25 x 10)cm = 250 cm
Now, semi-perimeter, s = 540/2cm = 270 cm
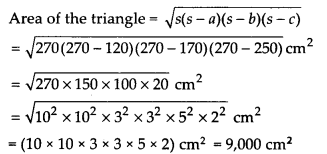
Ex 12.1 Class 9 Maths Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
Let the sides of an isosceles triangle be
a = 12cm, b = 12cm,c = x cm
Since, perimeter of the triangle = 30 cm
∴ 12cm + 12cm + x cm = 30 cm
⇒ x = (30 – 24) = 6
Now, semi-perimeter, s = 30/2cm =15 cm
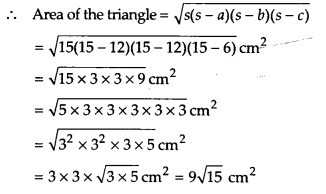
Thus, the required area of the triangle = 9√15 cm2
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Ex 12.2
Ex 12.2 Class 9 Maths Question 1.
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9m,BC = 12m,CD = 5m and AD = 8 m.
How much area does it occupy?
Solution:
Given, a quadrilateral ABCD with ZC = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m.
Let us join B and D, such that ABCD is a right angled triangle.
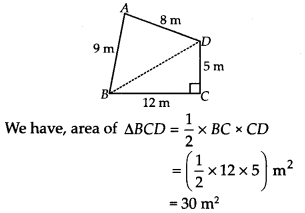
Now, to find the area of ∆ABD, we need the length of BD.
In right-angled ∆BCD, by Pythagoras theorem
BD2 = 502 + CD2
⇒ BD2 = 122 + 52
⇒ BD2 = 144 + 25 = 169
⇒ BD = 13 m
Now, for ∆ABD, we have
a = AB = 9 m, b = AD = 8 m, c = BD = 13 m

∴ Area of quadrilateral ABCD = area of ∆BCD + area of ∆ABD = 30 m2 + 35.5 m2
= 65.5 m2 (approx.)
Ex 12.2 Class 9 Maths Question 2.
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
Given a quadrilateral ABCD with AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
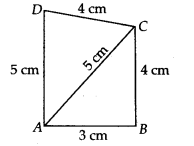
For ∆ABC, a = AB = 3 cm, b = BC = 4 cm and c = AC = 5 cm

Now, area of quadrilateral ABCD = area of ∆ABC + area of ∆ACD
= 6 cm2 + 9.2 cm2 = 15.2 cm2 (approx.)
Ex 12.2 Class 9 Maths Question 3.
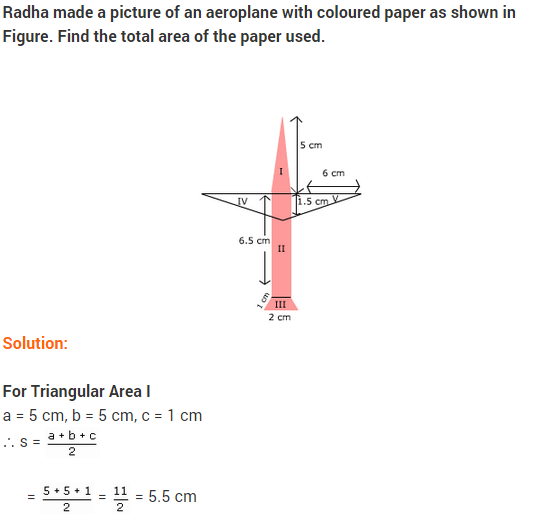
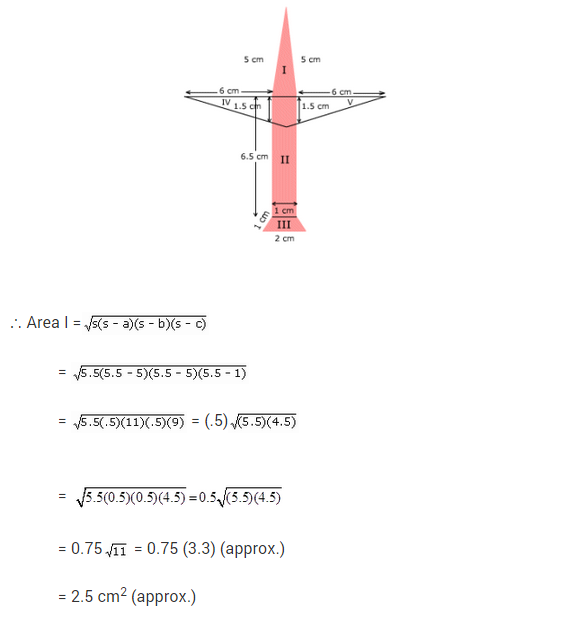
Radha made a picture of an aeroplane with coloured paper as shown in figure. Find the total area of the paper used.
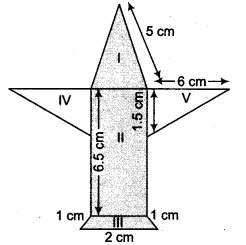
Solution:
For surface I:
It is an isosceles triangle whose sides are a = 5 cm, b = 5 cm, c = 1 cm
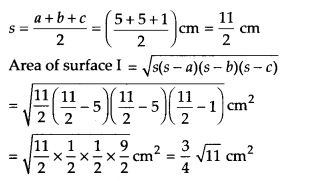
= (0.75 x 3.3) cm2
= 2.475 cm2 (approx.)
For surface II:
It is a rectangle with length 6.5 cm and breadth 1 cm.
∴ Area of surface II = Length x Breadth
= (6.5 x 1) cm2 = 6.5 cm2
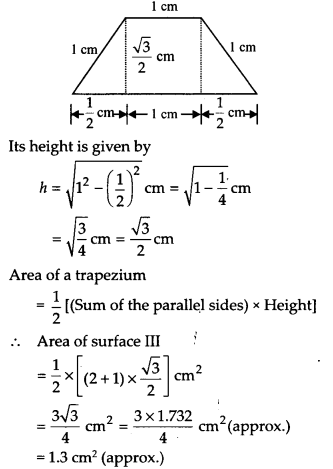
For surface III:
It is a trapezium whose parallel sides are 1 cm and 2 cm as shown in the figure given below:
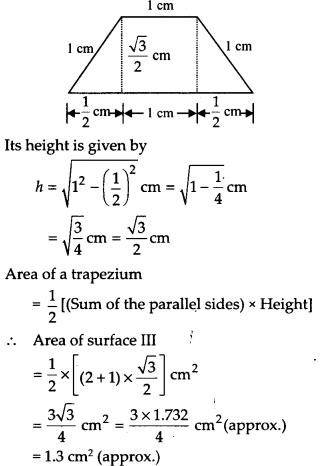
For surface IV and V:
Surface V is a right-angled triangle with base 6cm arid height 1.5 cm.
Also, area of surface IV = area of surface V
= 1/2 x base x height
= (1/2 x 6 x 15) cm2 = 4.5 cm2
Thus, the total area of the paper used = (area of surface I) + (area of surface II) + (area of surface III) + (area of surface IV) + (area of surface V) = [2.475 + 6.5 + 1.3 + 4.5 + 4.5] cm2
= 19.275 cm2
= 19.3 cm2 (approx.)
Ex 12.2 Class 9 Maths Question 4.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram
Solution:
For the given triangle, we have a = 28 cm, b = 30 cm, c = 26 cm
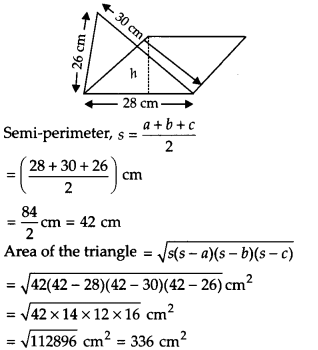
Area of the given parallelogram = Area of the given triangle
∴ Area of the parallelogram = 336 cm2
⇒ base x height = 336
⇒ 28 x h = 336, where ‘h’ be the height of the parallelogram.
⇒ h = 336/28 = 12
Thus, the required height of the parallelogram = 12 cm
Ex 12.2 Class 9 Maths Question 5.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution:
Here, each side of the rhombus = 30 m.
Let ABCD be the given rhombus and the diagonal, BD = 48 m
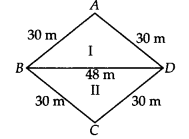
Sides ∆ABC are a = AB = 30m, b = AD = 30m, c = BD = 48m

Since, a diagonal divides the rhombus into two congruent triangles.
∴ Area of triangle II = 432 m2
Now, total area of the rhombus = Area of triangle I + Area of triangle II
= 432 m2 + 432 m2= 864 m2
Area of grass for 18 cows to graze = 864 m2
⇒ Area of grass for 1 cow to graze = 864/18 m2
= 48 m2
Ex 12.2 Class 9 Maths Question 6.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
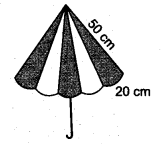
Solution:
Let the sides of each triangular piece be
a = 20 cm, b = 50 cm, c = 50 cm

Ex 12.2 Class 9 Maths Question 7.
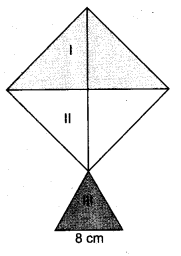
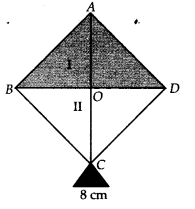
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in figure. How much paper of each shade has been used in it?
Solution:
Each shade of paper is divided into 3 triangles i.e., I, II, III
8 cm
For triangle I:
ABCD is a square [Given]
∵ Diagonals of a square are equal and bisect each other.
∴ AC = BD = 32 cm
Height of AABD = OA = (1/2 x 32 )cm
= 16 cm
Area of triangle I = (1/2 x 32 x 16 ) cm2
= 256cm2
For triangle II:
Since, diagonal of a square divides it into two congruent triangles.
So, area of triangle II = area of triangle I
∴ Area of triangle II = 256 cm2
For triangle III:
The sides are given as a = 8 cm, b = 6 cm and c = 6 cm
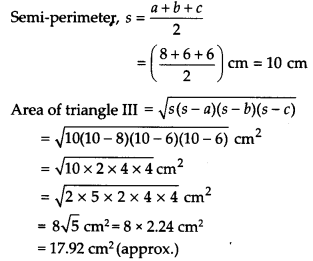
Thus, the area of different shades are:
Area of shade I = 256 cm2
Area of shade II = 256 cm2
and area of shade III = 17.92 cm2
Ex 12.2 Class 9 Maths Question 8.
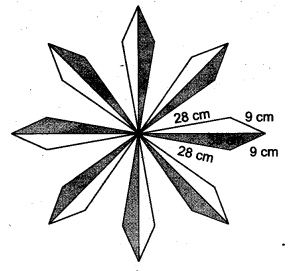
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see figure). Find the cost of polishing the tiles at the rate of 50 paise per cm .
Solution:
Let the sides of the triangle be a = 9 cm, b = 28 cm, c = 35 cm

Total area of all the 16 triangles = (16 x 88.2) cm2 = 1411.2 cm2 (approx.)
Cost of polishing the tiles = Rs. 0.5 per cm2
∴ Cost of polishing all the tiles = Rs. (0.5 x 1411.2) = Rs. 705.60 (approx.)
Ex 12.2 Class 9 Maths Question 9.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
Let the given field is in the form of a trapezium ABCD such that parallel sides are AB = 10 m and DC = 25 m
Non-parallel sides are AD = 13 m and BC = 14 m.
We draw BE || AD, such that BE = 13 m.
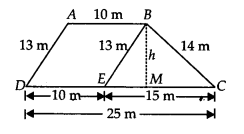
The given field is divided into two shapes (i) ∆BCE, (ii) parallelogram ABED For ∆BCE:
Sides of the triangle are a = 13 m, b = 14 m, c = 15 m
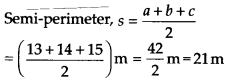
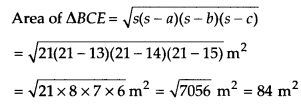
(ii) For parallelogram ABED:
Let the height of the ∆BCE corresponding to the side EC be h m.
Area of a triangle = 1/2 x base x height
∴ 1/2 x 15 x h = 84
⇒ (10 + 82×2/15 = 56/5
Now, area of a parallelogram = base x height
= (10 x 56/5) = (2 x 56) m2 = 112 m2
So, area of the field
= area of ∆BCE + area of parallelogram ABED
= 84 m2 + 112 m2 = 196 m2
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula Ex 12.2
Ex 12.2 Class 9 Maths Question 1

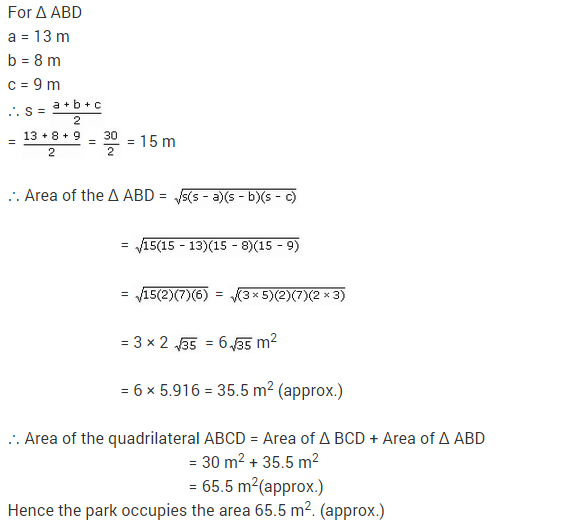
Ex 12.2 Class 9 Maths Question 2


Ex 12.2 Class 9 Maths Question 3

Ex 12.2 Class 9 Maths Question 4

Ex 12.2 Class 9 Maths Question 5



Ex 12.2 Class 9 Maths Question 6

Ex 12.2 Class 9 Maths Question 7

![]()
Ex 12.2 Class 9 Maths Question 8

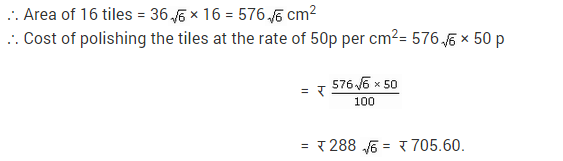
Ex 12.2 Class 9 Maths Question 9


Heron’s formula Class 9 Extra Questions Maths Chapter 12
Extra Questions for Class 9 Maths Chapter 12 Heron’s formula











IMPORTANT QUESTIONS
VERY SHORT ANSWER TYPE QUESTIONS
Question.1 Two parallelograms are on equal bases and between the same parallels. Find the ratio of their areas.
Solution. 1:1 [...Two Parallelograms on the equal based and between the same parallels are equal in area.]
Question.2 If a triangle and a parallelogram are on same base and between same parallels, then find the ratio of the area of the triangle to the area of parallelogram.
Solution. 1 : 2 [... If a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to half of the parallelogram.]
Question.3

Solution.

Question.4.

Solution.

Question.5

Solution.

Question.6 In the given figure, D is the mid-point of BC and L mid-is the point of AD. If ar(ΔABL) = x ar(ΔABC), then find the value of x

Solution.

Question.7

Solution.

Question.8

Solution.


Question.9

Solution.

Question.10

Solution.

Question.11 In figure, TR ⊥ PS, PQ // TR and PS // QR. If QR = 8 cm, PQ = 3 cm and SP = 12 cm, find arquad. PQRS).[CBSE-14-17DIG1U]
Solution.

Question.12
 ]
]
Solution.

Question.13

Solution.

Question.14

Solution.


SHORT ANSWER QUESTIONS TYPE-I
Question.15

Solution.

Question.16

Solution.

Question.17 Prove that parallelogram on equal bases and between the same parallels are equal in area. [CBSE March 2012]
Solution.

Question.18

Solution.

Question.19

Solution.


Question.20

Solution.

Question. 21

Solution.


Question.22 ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(ΔAOD) = 4 cm2, find area of parallelogram ABCD. [CBSE-14-GDQNI3W]
Solution.

Question.23

Solution.

Question.24

Solution.

Question.25

Solution.

SHORT ANSWER QUESTI-IIONS TYPE
Question. 26 A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it ?
Solution.

Question.27

Solution.

Question.28 InΔPQR, A and B are points on side QR such that they trisect QR. Prove that
ar(ΔPQB) = 2ar(ΔPBR).
Solution.

Question.29 For the given figure, check whether the following statement is true or false. Also justify your answer. PQRS is a trapezium with PQ // SR, PS // RU and ST // II RQ, then ar(PURS) = ar(TQRS)
[CBSE-14-ERFKZ8H]

Solution.

Question.30 In the given figure, WXYZ is a quadrilateral with a point P on side WX. If ZY // WX, show that :
(i) ar(ΔZPY) = ar(ΔZXY)
(ii)ar(ΔWZY) = ar(ΔAZPY)
(iii)ar(ΔZWX) = ar(ΔXWY) [CBSE-14-ERFKZ8H]

Solution.

Question.31. Triangles ABC and DBC are on the same base BC and A, D on the opposite sides of BC, such that ar(ΔABC) = ar(ΔDBC), show that BC bisect AD.
Solution.


Question.32 Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) X ar(ΔBPC).
Solution.

Question.33 The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q, then parallelogram PBQR is completed (see figure). Show that ar(∥gmABCD) = ar(∥gmABCD).
[CBSE March 2012]

Solution.

LONG ANSWER TYPE QUESTIONS
Question.34. ΔBCD is a parallelogram and P is any point in its interior. Show that ar(ΔAPB) + ar(ΔCPD)= ar(ΔBPC) + ar(ΔAPD) [CBSE-15-6DWMW5A)

Solution.


Question.35 In the given figure, ABCD is a square. Side AB is produced to points P and Q in such a way that PA = AB = BQ. Prove that DQ = CP.[CBSE-15-NS72LP7]

Solution.

Question.36 EFGH is a parallelogram and U and T are points on sides EH and GF respectively. If ar(ΔEHT) = 16 cm2, find ar(ΔGUF) [CBSE-15-NS72LP7]

Solution.

Value Based Questions (Solved)
Question.1 A farmer having afield in the form of parallelogram PQRS.
He planned to built a home for old persons of the village in the field leaving open portion equal to portion covered by the home. For this he divided the field by taking a point A on RS and joining AP, AQ respectively as shown in figure.
(i) How should he do it ?
(ii)What values are depicted in his plan ?

Solution.

Question.2 Naveen was having a plot in the shape of a quadrilateral. He decided to donate some portion of it to construct a home for orphan girls. Further he decided to buy a land in lieu of his donated portion of his plot so as to form a triangle.
(i) Explain how this proposal will be implemented ?
(ii)Which mathematical concept is used in it ?
(iii)What values are depicted by Naveen ?
Solution.

(ii) Area of parallelogram and triangle and mid-point theorem.
(iii) Every child, boy or girl have equal right, so avoid discrimination in boy and girl.
Question.3 Mr Sharma explains his four children two boys and two girls about distribution of his property among them by a picture of A ABC such that D, E, F are mid-points of sides AB, BC, CA respectively are joined to divide A ABC in four triangles as shown in figure.
(i) If total property is equal to area of A ABC and share of each child is equal to area of each of four triangles, what does each child has share ?
(ii)Which mathematical concept is used in it ?
(iii)Which values are depicted in Mr Sharma’s plan ?

Solution.

Question.4 A flood relief camp was organized by state government for the people affected by the natural calamity near a city. Many school students volunteered to participate in the relief work. In the camp, the food items and first aid centre kits were arranged for the flood victims.
The piece of land used for this purpose is shown in the figure.
(a) If EFGH is a parallelogram with P and Q as mid-points of sides GH and EF respectively, then show that area used for first aid is half of the total area.
(b) What can you say about the student volunteers working for the relief work ?
[CBSE-14-GDQNI3W]

Solution.

Question.5 Sunita has a plot of land which she decides to use for building an old age home and a dispensary for the needy. Her plot is shown in the figure. Plot ABCD is a parallelogram
(a) If R is point on diagonals BD. Show that equal areas allotted for building old age home and the dispensary.
(b) What value is depicted by the above situation ?

Solution.

