NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.1
Ex 13.1 Class 9 Maths Question 1.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1m2 costs ₹20.
Solution:
(i) Here, length (l) = 1.5 m, bread th(b) = 1 .25 m
and height (h) = 65 cm = 65/100 m = 0.65 m
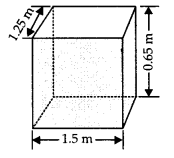
∵ It is open from the top.
∴ Its surface area
= [Lateral surface area] + [Base area]
= [2(1 + b)h] + [lb]
= [2(1.50 + 1.25)0.65] m2 + [1.50 x 1.25] m2
= [2 x 2.75 x 0.65] m2 + [1.875] m2
= 3.575 m2+ 1.875 m2 = 5.45 m2
∴ Area of the sheet required for making the box = 5.45 m2
(ii) Cost of 1 m2 sheet = Rs. 20
Cost of 5.45 m2 sheet = Rs. (20 x 5.45)
= Rs. 109
Hence, cost of the required sheet = Rs. 109
Ex 13.1 Class 9 Maths Question 2.
The length, breadth and height of a room are 5 m, 4 m and 3 m, respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of ₹17.50 per m2.
Solution:
Length of the room (l) = 5 m
Breadth of the room (b) = 4 m
Height of the room (h) = 3 m
The room is like a cuboid whose four walls (lateral surface) and ceiling are to be white washed.
∴ Area for white washing
= [Lateral surface area] + [Area of the ceiling]
= [2(l + b)h] + [l x b]
= [2(5 + 4) x 3] m2 + [5 x 4] m2 = 54 m2 + 20 m2 = 74 m2
Cost of white washing for 1 m2 area = Rs. 7.50
∴ Cost of white washing for 74 m2 area = Rs. (7.50 x 74) = Rs. 555
Thus, the required cost of white washing = Rs. 555
Ex 13.1 Class 9 Maths Question 3.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹10 per m2 is ₹15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area]
Solution:
A rectangular hall means a cuboid.
Let the length and breadth of the hall be l and b respectively.
∴ Perimeter of the floor = 2(l + b)
⇒ 2(l + b) = 250 m
∵ Area of four walls = Lateral surface area = 2(1 + b) x h, where h is the height of the hall = 250 h m2
Cost of painting the four walls
= Rs. (10 x 250 h) = Rs. 2500h
⇒ 2500 h = 15000 ⇒ h = 15000/2500 = 6
Thus, the required height of the hall = 6 m
Ex 13.1 Class 9 Maths Question 4.
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm x 10 cm x 7.5 cm can be painted out of this container.
Solution:
Total area that can be painted = 9.375 m2
Here, Length of a brick (l) = 22.5 cm
Breadth of a brick (b) = 10 cm
Height of a brick (h) = 7.5 cm
Since a brick is like a cuboid, then
Total surface area of a brick = 2[lb + bh + hl]
= 2[(225 x 1(0) + (10 x 7.5) + (7.5 x 22.5)] cm2
= 2[(225) + (75) + (168.75)] cm2
= 2[468.75] cm2 = 937.5 cm2 = 937.5/10000 m2
Let the required number of bricks be n
∴ Total surface area of n bricks = n x 937.5/10000 m2
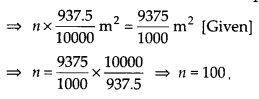
Thus, the required number of bricks = 100
Ex 13.1 Class 9 Maths Question 5.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
Solution:
For the cubical box with edge (a) = 10 cm
Lateral surface area = 4a2 = 4 x 102 cm2
= 400 cm2
Total surface area = 6a2 = 6 x 102 cm2
= 600 cm2
For the cuboidal box with dimensions,
Length (l) = 12.5 cm,
Breadth (b) = 10 cm,
Height (h) = 8 cm
∴ Lateral surface area = 2[l + b] x h = 2[12.5 + 10] x 8 cm2 = 360 cm2
Total surface area = 2[lb + bh + hl]
= 2[(12.5 x 10) + (10 x 8) + (8 x 12.5)] cm2
= 2[125 + 80 + 100] cm2
= 2[305] cm2
= 610 cm2
(i) A cubical box has the greater lateral surface area by (400 – 360) cm2 = 40 cm2.
(ii) Total surface area of a cubical box is smaller than the cuboidal box by (610 – 600) cm2 = 10 cm2.
Ex 13.1 Class 9 Maths Question 6.
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
Solution:
The herbarium is like a cuboid.
Here, length (l) = 30 cm,
breadth (b) = 25 cm,
height (h) = 25 cm
(i) Surface area of the herbarium (glass)
= 2[lb + bh + hl]
= 2[(30 x 25) + (25 x 25) + (25 x 30)] cm2 – 2[750 + 625 + 750] cm2
= 2[2125] cm2
= 4250 cm2
Thus, the required area of the glass = 4250 cm2
(ii) Total length of 12 edges = 4l + 4b + 4h
= 4(l + b + h)
= 4(30 + 25 + 25) cm
= 4 x 80 cm = 320 cm
Thus, the required length of tape = 320 cm
Ex 13.1 Class 9 Maths Question 7.
Shanti Sweets Stalll was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm x 20 cm x 5 cm and the smaller of dimensions 15 cm x 12 cm x 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is ₹4 for 1000 cm², find the cost of cardboard required for supplying 250 boxes of each kind.
Solution:
For bigger box:
Length (l) = 25 cm,
Breadth (b) = 20 cm,
Height (h) = 5 cm
Total surface area of a box = 2(lb + bh + hl)
= 2[(25 x 20) + (20 x 5) + (5 x t25)] cm2
= 2 [500 + 100 + 125] cm2
= 2[725] cm2
= 1450 cm2
Total surface area of 250 boxes = (250 x 1450) cm2 = 362500 cm2
For smaller box:
l = 15 cm, b = 12 cm, h = 5 cm
Total surface area of a box = 2 [lb + bh + hl]
= 2[(15 x 12) + (12 x 5) + (5 x 15)] cm2
= 2[180 + 60 + 75] cm2 = 2[315] cm2 = 630 cm2
∴ Total surface area of 250 boxes = (250 x 630) cm2 = 157500 cm2
Now, total surface area of both type of boxes = 362500 cm2 +157500 cm2 = 520000 cm2 Area for overlaps = 5% of [total surface area]
= 5/100 x 520000 cm2 = 26000 cm2
∴ Total surface area of the cardboard required = [Total surface area of 250 boxes of each type] + [Area for overlaps]
= 520000 cm2 + 26000 cm2 = 546000 cm2
∵ Cost of 1000 cm2 cardboard = Rs. 4
∴ Cost of 546000 cm2 cardboard
= Rs.4×546000/1000 = Rs. 2184
Ex 13.1 Class 9 Maths Question 8.
Parveen wanted to make a temporary shelter, for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m x 3 m?
Solution:
Here, length (l) = 4 m,
breadth (b) = 3m
and height (h) = 2.5 m
The structure is like a cuboid.
∴ The surface area of the cuboid, excluding the base
=[Lateral surface area] + [Area of ceiling]
= [2(l + b)h] + [lb]
= [2(4 + 3) x 2.5] m2 + [4 x 3] m2
= 35 m2 + 12 m2 = 47 m2
Thus, 47 m2 tarpaulin would be required.
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.2









NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3










NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4


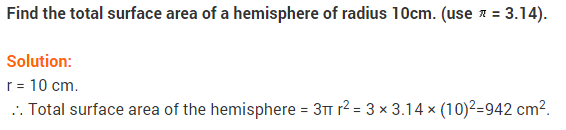






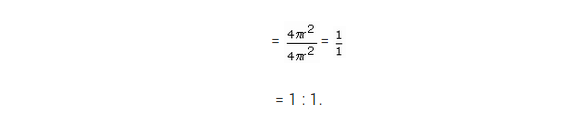
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5
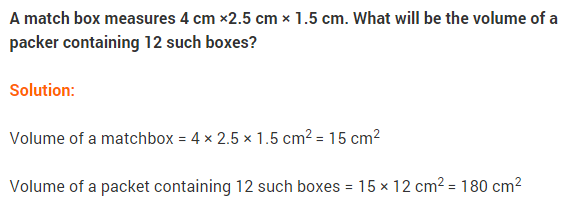









NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6








NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7

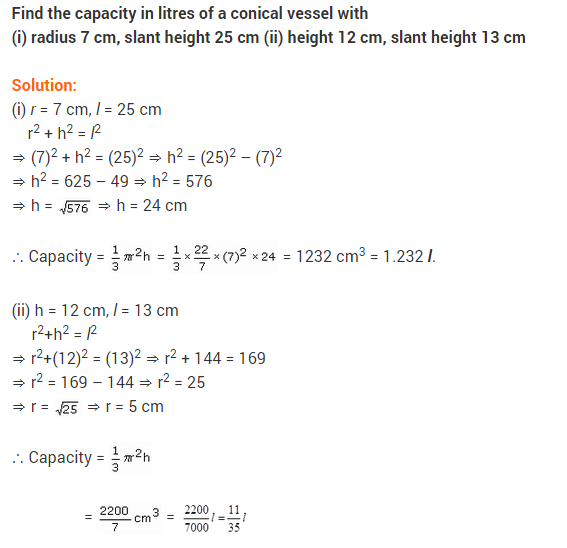








NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8













NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9
Ex 13.9 Class 9 Maths Question 1.
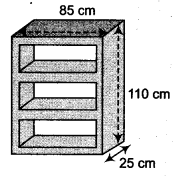
A wooden bookshelf has external dimensions as follows : Height = 110cm, Depth = 25cm, Breadth = 85cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing-is 20 paise per cm2 and the rate of pointing is 10 paise per cm2, find the total expenses required for palishing and painting the surface of the bookshelf.
Solution:
Here, l = 85 cm b = 25 cm and h = 110 cm
Area of the bookshelf of outer surface = 2 lb + 2bh + hl
= [2(85 x 25)+ 2(110 x 25)+ 85×110] cm2 = (4250 + 5500 + 9350) cm2 = 19100 cm2
Cost of polishing of the outer surface of bookshelf
= 19100 x 20/100 = ₹ 3820
Thickness of the plank = 5 cm
Internal height of bookshelf = (110 – 2 x 5) = 100 cm
Internal depth of bookshelf = (25 – 5) = 20 cm
Internal breadth of bookshelf = 85 – 2 x 5 = 75 cm
Hence, area of the internal surface of bookshelf
= 2(75 x 20)+ 2(100x 20)+ 75×100
= 3000 + 4000 + 7500 = 14500 cm2
So, cost of painting of internal surface of bookshelf
= 14500 x 10/100 = ₹1450
Hence, total costing of polishing and painting = 3820 + 1450= ₹ 5270
Ex 13.9 Class 9 Maths Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in figure. Eight such spheres are-used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.
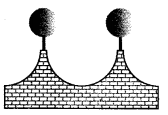
Solution:
It is obvious, we have to subtract the cost of the sphere that is resting on the supports while calculating the cost of silver paint.
Surface area to be silver paint
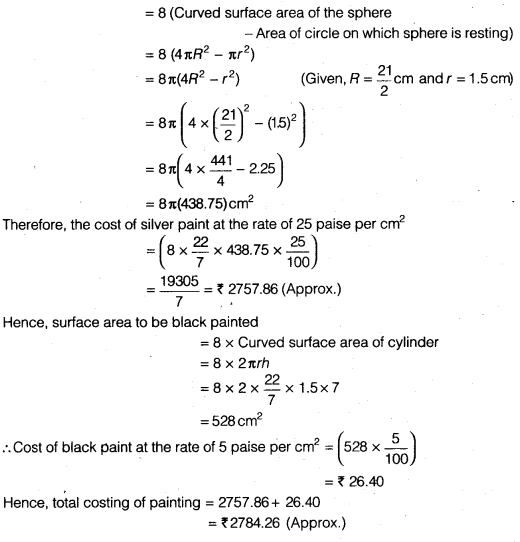
Ex 13.9 Class 9 Maths Question 3.
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Solution:
Let d be the diameter of the sphere


Surface Areas and Volumes Class 9 Extra Questions Maths Chapter 13
Extra Questions for Class 9 Maths Chapter 13 Surface Areas and Volumes
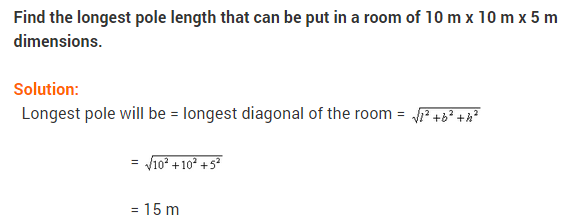
































IMPORTANT QUESTIONS
VERY SHORT ANSWER TYPE QUESTIONS
1. How much ice-cream can be put into a cone with base radius 3.5 cm and height 12 cm ? [CBSE-14-GDQNI3W]
Answer.

2. The total surface area of a cube is 726 cm2. Find the length of its edge. [CBSE-14-ERFKZ8H]
Answer.

3. If a wooden box of dimensions 8 m x 7 m x 6 m is to carry boxes of dimensions 8 cm x 7 cm x 6 cm, then find the maximum number of boxes that can be carried in the wooden box. [CBSE-14-GDQNI3W]
Answer.

4. Two cubes of edge 6 cm are joined to form a cuboid. Find the total surface area of the cuboid. [CBSE-15-NS72LP7]
Answer. When two cubes are joined end to end, then
Length of the cuboid = 6 + 6 = 12 cm
Breadth of the cuboid = 6 cm
Height of the cuboid = 6 cm
Total surface area of the cuboid = 2 (lb + bh + hi)
= 2(12 x6 + 6×6 + 6×12)
= 2(72 + 36 + 72) = 2(180) = 360 cm2
5. Calculate the edge of the cube if its volume is 1331 cm3. [CBSE-15-6DWMW5A]
Answer.

6. If in a cylinder, radius is doubled and height is halved, then find its curved surface area.
Answer.

7. The radii of two cylinders of the same height are in the ratio 4 :5, then find the ratio of their volumes.
Answer.

8. Find the area of the sheet required to make closed cylindrical vessel of height 1 m and diameter 140 cm.
Answer.

9. Find the volume of cone of radius r/2 and height ‘2h’.
Answer.

10. How many balls, each of radius 2 cm can be made from a solid sphere of lead of radius 8 cm ? [CBSE-14-17DIG1U]
Answer.

11. A cone is 8.4 cm high and the radius of its base is 2.1 cm. It is melted and recast into a sphere. Find the radius of the sphere.[NCERT Exemplar Problem]
Answer.

12. If the volume of a sphere is numerically equal to its surface area, then find the diameter of the sphere.
Answer.

13. The radius of a spherical balloon increases from 6 cm to 12 cm as air is being pumped into it. Then what will be the ratio of surface areas of the original balloon to the resulting new balloon ?
Answer.

14. The outer and the inner radii of a hollow sphere are 12 cm and 10 cm. Find its volume. [CBSE-14-17DIG1U]
Answer. Inner radius of hollow sphere (r) = 10 cm Outer radius of hollow sphere (R) = 12 cm

15. In a cylinder, if radius is halved and height is doubled, then find the volume with respect to original volume. [NCERT Exemplar Problem]
Answer.

SHORT ANSWER QUESTIONS TYPE-I
16. A spherical ball is divided into two equal halves. If the curved surface area of each half is 56.57 cm?, find the volume of the spherical ball. [use π = 3.14] [CBSE-14-GDQNI3W]
Answer.

17. Find the length of the longest pole that can be put in a room of dimensions 10 m x 10 m x 5 m. [NCERT Exemplar Problem]
Answer. Here, we have a cuboid with dimensions
l= length = 10 m, b = breadth = 10 m and h = height = 5 m
Now, length of longest pole = diagonal of cuboid

18. Find the capacity in litres of a conical vessel having height 8 cm and slant height 10 cm. [CBSE-15-6DWMW5A]
Answer.

19. Calculate the surface area of a hemispherical dome of a temple with radius 14 m to be whitewashed from outside. [CBSE -15-NS72LP7]
Answer.

20. A school provides milk to the students daily in cylindrical glasses of diameter 7 cm. If the glass is filled with milk up to a height of 12 cm, find how many litres of milk is needed to serve 1600 students. [CBSE March 2011]
Answer.

21. A rectangular piece of paper is 22 cm long and 10 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder. [CBSE-14-ERFKZ8H]
Answer.

22. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find it volume. If 1cm3 wheat cost is Rs 10, then find total cost. [CBSE-14-GDQNI3W]
Answer.

23. A shot-put is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g/cm3. Find the mass of the shot-put. [CBSE March 2012]
Answer.

24. A cylindrical vessel can hold 154 g of water. If the radius of its base is 3.5 cm, and 1 cm3 of water weighs lg,find the depth of water. [CBSE-14-17DIG1U]
Answer.


SHORT ANSWER QUESTIONS TYPE-II
25. A wall of length 10 m is to be built across an open ground. The height of the wall is 5 m and thickness of the wall is 42 cm. If this wall is to be built with bricks of dimensions 42 cm x 12 cm x 10 cm, then how many bricks would be required ? [CBSE-14-ERFKZ8H] [CBSE-15-NS72LP7]
Answer.

26. The curved surface area of a cylinder is 176 cm2 and its area of the base is 38.5 cm2. Find the volume of the cylinder. (Take π = 22/7) [CBSE March 2012]
Answer.

27. The diameter of a roller is 42 cm and its length is 120 cm. It takes 500 complete revolutions to move once to land a playground. Find the area of the playground in m2. [CBSE March 2012]
Answer.

28. Rinku has built a cuboidal water tank in his house. The top of the water tank is covered with an iron lid. He wants to cover the inner surface of the tank including the base with tiles of size 10 cm by 8 cm. If the dimensions of the water tank are 180 cm x 120 cm x 60 cm and cost of tiles is f 480 per dozen, then find the total amount required for tiles. [CBSE March 2012]
Answer.

29. The diameter of moon is approximately 1/4 th of the diameter of earth. What fraction of volume of earth is the volume of moon ? [CBSE March 2012]
Answer.


30. The curved surface area of a cylinder is 154 cm2. The total surface area of the cylinder is three times its curved surface area. Find the volume of the cylinder. [CBSE-14-GDQNI3W]
Answer.

31. A right angled A ABC with sides 3 cm, 4 cm and 5 cm is revolved about the fixed side of 4 cm. Find the volume of the solid generated. Also, find the total surface area of the solid. [CBSE-14-17DIG1U]
Answer.

32. Curved surface area of cylindrical reservoir 12 m deep is plastered from inside with concrete mixture at the rate of Rs 15 per m2. If the total payment made is of Rs 5652, then find the capacity of this reservoir in litres. [CBSE-14-GDQNI3W]
Answer.

33. How many metres of 5 m wide cloth will be required to make a conical tent, the radius of whose base is 3.5 m and height is 12 m ? [CBSE March 2011 ]
Answer.

34. A shopkeeper has one spherical laddoo of radius 5 cm. With the same amount of material, how many laddoos of radius 2.5 cm can be made ? [NCERT Exemplar Problem]
Answer.


35. A semicircular sheet of metal of radius 14 cm is bent to form an open conical cup. Find the capacity of the cup.
Answer.

LONG ANSWER TYPE QUESTIONS
36. A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height ?[NCERT Exemplar Problem]
Answer. Let ‘r’ be the radius of sphere and right circular cylinder with height ‘h’. According to the statement of question, we have

37. A cube and a cuboid have the same volume. The dimensions of the cuboid are in the ratio 1:2: 4. If the difference between the cost of painting the cuboid and cube (whole surface area) at the rate of Rs 5 per m2 is Rs 80. Find their volumes. [CBSE March 2012]
Answer.

38. Ajay has built a cubical witter tank in his house. The top of the water tank is covered with lid. He wants to cover the inner surface of the tank including the lid with square tiles of side 25 cm. If each inner edge of the water tank is 2 m long and tiles costs Rs 360 per dozen, then find the total amount required for tiles. [CBSE March 2012]
Answer.

39. A tent is in shape of a right circular cylinder up to a height of 3 m and a cone above it. The maximum height of the tent above ground is 13.5 m. Calculate the cost of painting the inner side of the tent at the rate of Rs 3 per sq. m, if the radius of the base is 14 m. [CBSE March 2011]
Answer.

40. Manoj Sweets placed an order of making 30 cm x 20 cm x 6 cm cardboard boxes for packing their sweets. For all overlaps, 5 % of total area is required extra. If cost of the cardboard is Rs 2 for 1000 cm2 , find the cost of the cardboard used for making 500 boxes. [CBSE-14-17DIG1U]
Answer.

41. A cylindrical bucket 32 cm high and with base diameter 36 cm is filled with wheat. This bucket is emptied on the ground and a conical heap is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.[CBSE-14-ERFKZ8H]
Answer.

42. Using clay, Anant made a right circular cone of height 48 cm and base radius 12 cm. Versha reshapes it in the form of a sphere. Find the radius and curved sutface area of the sphere so formed. [CBSE-15-6DWMW5A]
Answer.

43. A metallic right circular cylinder is 15 cm high and the diameter of its base is 14 cm. It is melted and recasted into another cylinder with radius 4 cm. Find its height and curved surface area of the new cylinder. [CBSE-14-17DIG1U]
Answer.


44. A spherical metallic shell with 10 cm external diameter weighs 1789 1/2 g. Find the thickness of the shell, if the density of the metal is 7g/cm3. [CBSE-15-6DWMW5A], [CBSE-15-NS72LP7]
Answer. External radius of metallic shell (R) = 5 cm
Let internal radius of metallic shell be r.

45. A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of Rs 498.96. If the rate of whitewashing is Rs 4 per square metre, find the :
(i) Inside surface area of the dome
(ii) Volume of the air inside the dome [CBSE-15-6DWMW5A]
Answer. Here, dome of building is a hemisphere.
Total cost of white washing inside the dome = Rs 498.96
Rate of whitewashing = Rs 4 per m2

Value Based Questions
1. A residential house society is built is 4000 sq. m area. It has an underground tank to collect the rain water, the length, breadth and height of which are 50 m, 40 m and 4 m respectively. If it rains at the rate of 2 mm per minute for 5 hours, then calculate the depth of water in the tank. What value is depicted in this problem ? [CBSE-15-6DWMW5A]
Answer.

2. A village having a population of 4000 requires 150 litres of water per head per day. Due to lack of sources of water, they collect the water into a tank measuring 20 m x 15 m x 6 m from a river using a long pipe.
(i) For how many days will the water of this tank last ?
(ii) Which message is conveyed by the people of village ?
Answer.

3. Arihant builds a room measuring roof 22 m by 20 m. He also builds a cylindrical tank having diameter of base 2 m and height 3.5 m adjoining the room to collect the rainwater of roof for harvesting. If the tank is just filled with rainwater, find the rainfall in cm. What values are depicted in Arihant’s plan ?
Answer.

4. Naresh, a juice seller has set up his juice shop. He has three types of glasses (see figure) of inner diameter 5 cm to serve the customers. The height of the glasses is 10 cm.

He decided to serve the customer in ‘A’ type of glasses. (Take π = 3.14)
(i) Find the volume of each type of glass.
(ii) Which glass has the minimum capacity ?
(iii) Which mathematical concept is used in above problem ?
(iv) By choosing a glass of type A, which value is depicted by juice seller Naresh?
Answer.

