NCERT Solutions for Class 9 Maths Chapter 14 Statistics
NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.1
Ex 14.1 Class 9 Maths Question 1.
Give five examples of data that you collect from your day-to-day life.
Solution:
Following are the five examples which are related to day-to-day life :
- Number of girl students in our class.
- Number of computer sets in our computer lab.
- Telephone bills of our house for last two years.
- Number of students appeared in an examination obtained from newspapers.
- Number of female teachers in all the schools in a state obtained from the education department.
Ex 14.1 Class 9 Maths Question 2.
Classify the data in Q.1 above as primary or secondary data.
Solution:
We have,
Primary data: (i), (ii) and (iii)
Secondary data: (iv) and (v)
NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.2
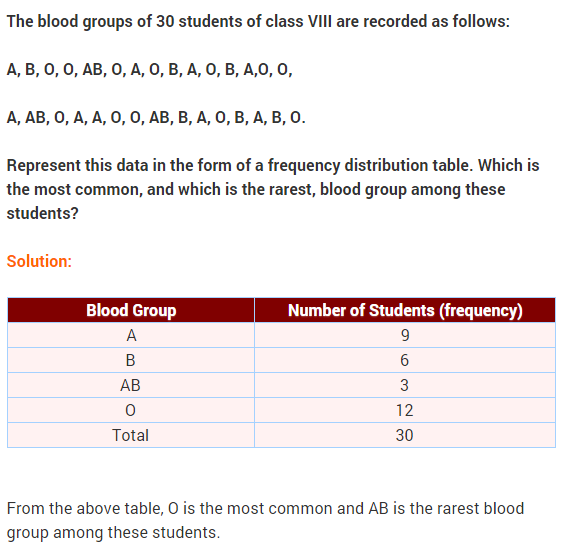
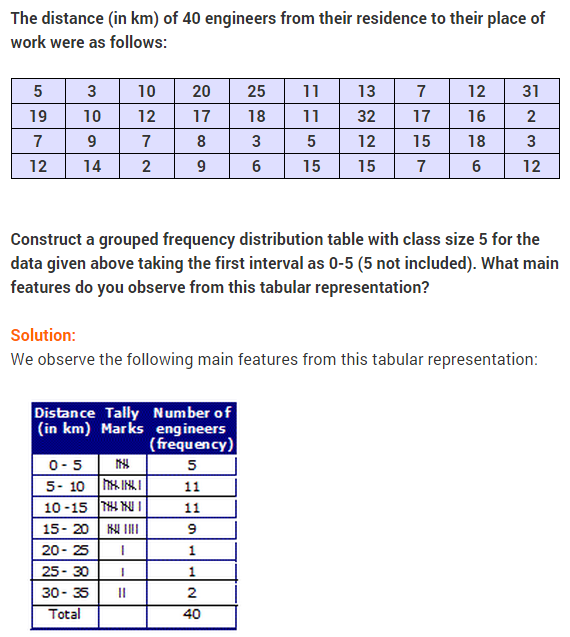

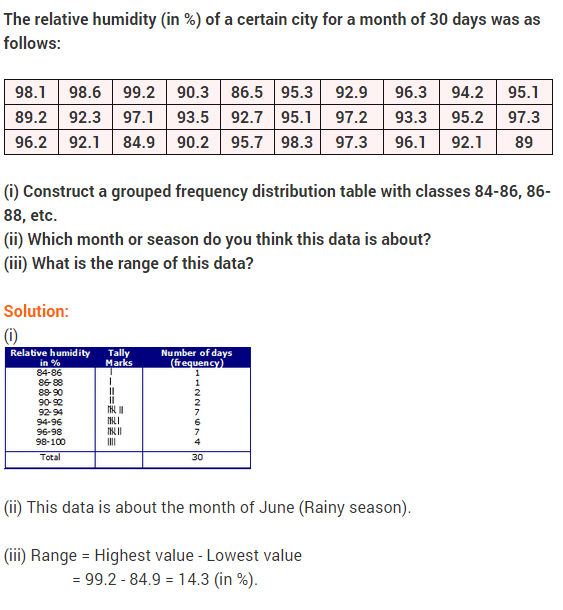
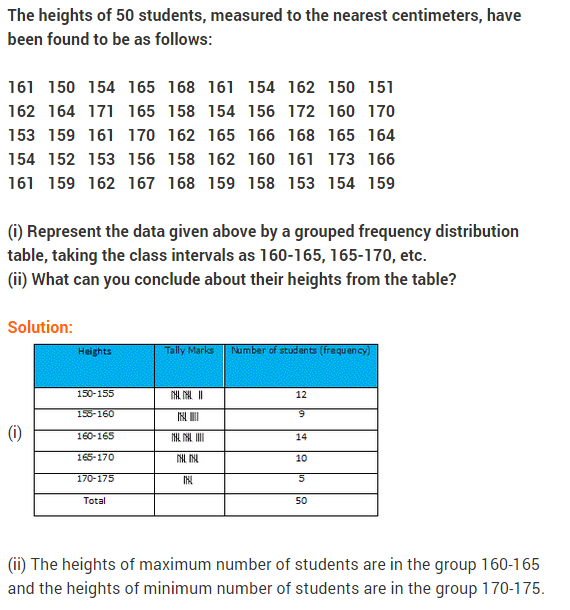

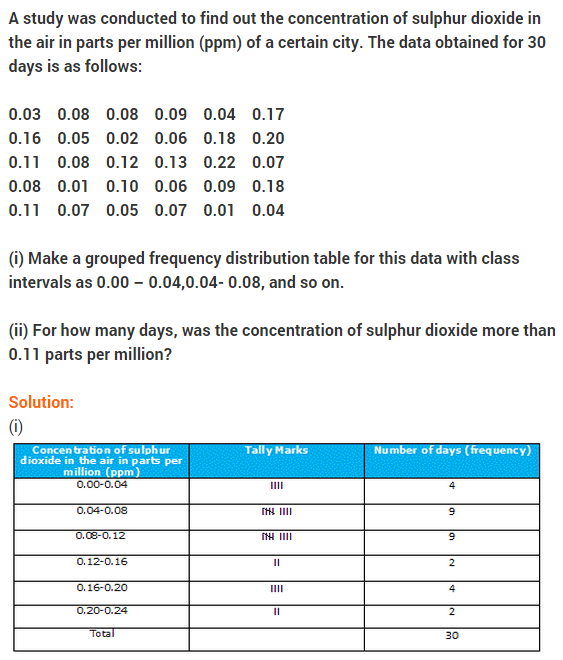
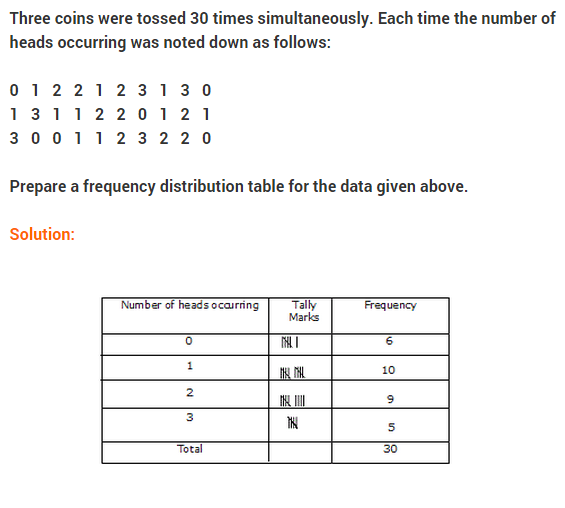



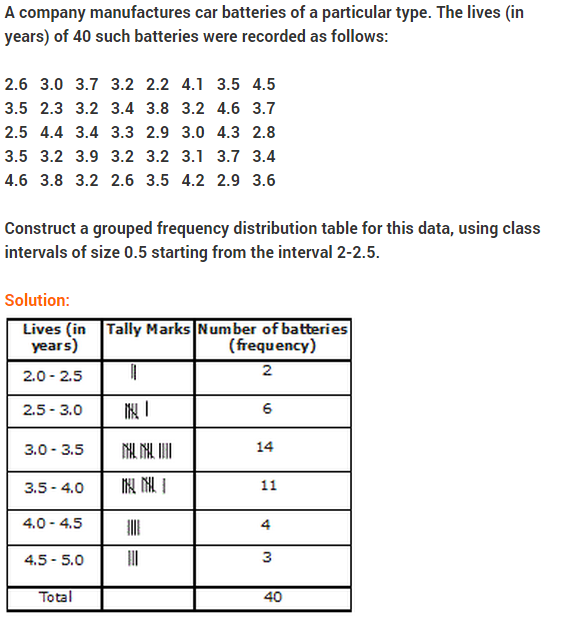
NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.3

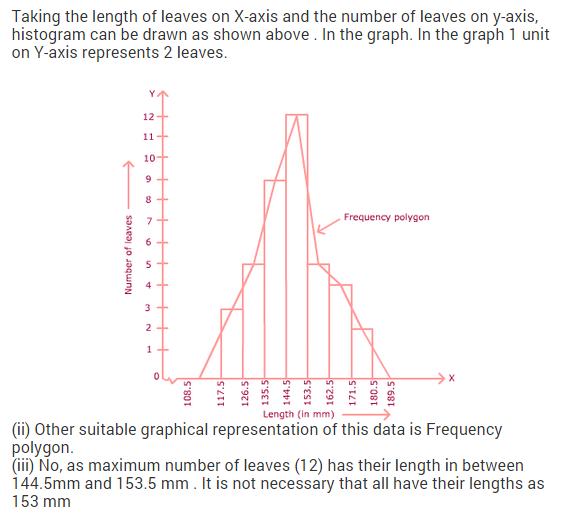
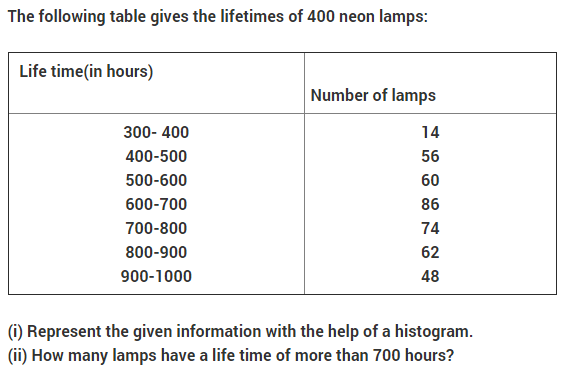
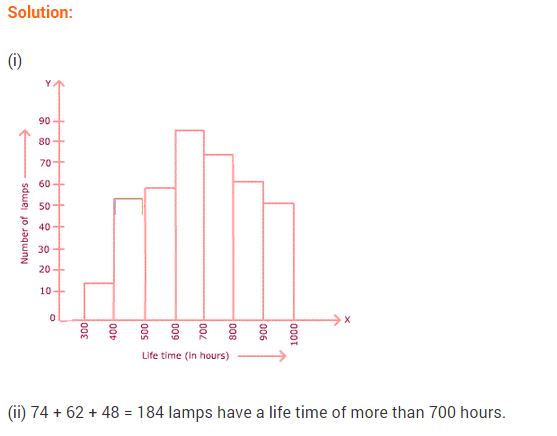
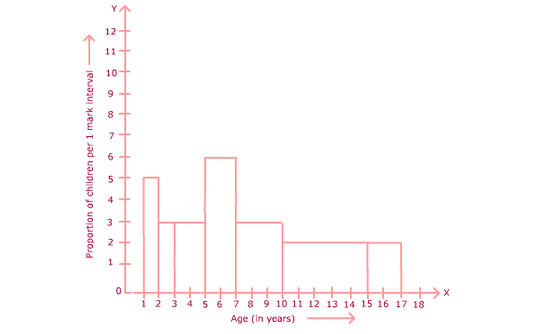
NCERT Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.4






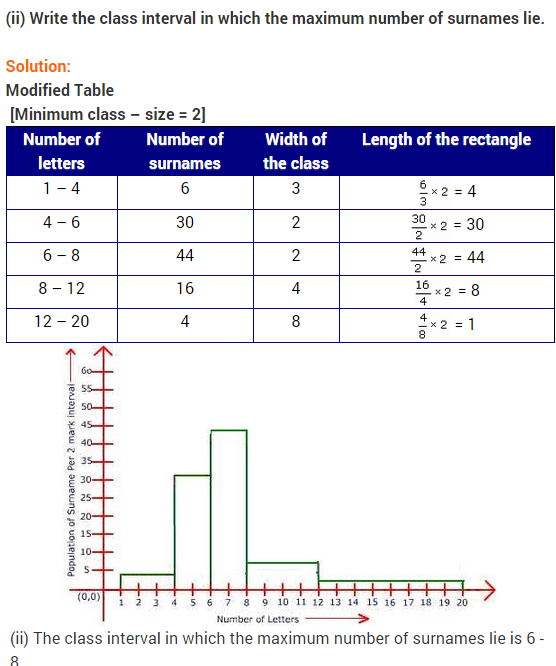
Statistics Class 9 Extra Questions Maths Chapter 14
Extra Questions for Class 9 Maths Chapter 14 Statistics
IMPORTANT QUESTIONS
VERY SHORT ANSWER TYPE QUESTIONS
1. Mean of 20 observations is 17. If in the observations, observation 40 is replaced by 12, find the new mean. [CBSE-14-ERFKZ8H]
Answer. Since mean of 20 observations is 17
Sum of the 20 observations = 17 x 20 = 340
New sum of 20 observations = 340 – 40 + 12 = 312
Newmean=312 / 20 =15.6
2. If the mean of the data x1,x2,x3…………….xn is x¯ ,then find the mean of αx1, αx2, αx3…………….αxn.
Answer.

3. Mean of 36 observations is 12. One observation 47 was misread as 74. Find the correct mean. [CBSE-14-17DIG1U]
Answer. Mean of 36 observations = 12
Total of 36 observations = 36 x 12 = 432
Correct sum of 36 observations = 432 – 74 + 47 = 405
Correct mean of 36 observations = 405/ 36 =11.25
4. If the mean of five observations x, x + 2, x + 4, x + 6, x + 8 is 11, then write the value of x.
Answer.

5. Determine the mean of first 10 natural numbers.
Answer. First ten natural numbers are 1, 2, 3. 4, 5, 6, 7, 8, 9 and 10

6. Find the mean of x, x + 2, x + 4, x + 6, x + 8.
Answer.

7. Write the class mark of an interval 90 – 120.
Answer. Classmark= (90+120 )/ 2 = 210 / 2 =105
8. The mean of 8 observations is 40. If 5 is added to each observation, then what will be the new mean ?
Answer.

9. Find the range of the given data : 25, 18, 20, 22, 16, 6, 17, 15, 12, 30, 32, 10, 19, 8, 11, 20
Answer. Here, the minimum and maximum values of given data are 6 and 32 respectively.
Range = 32 – 6 = 26
10. There are 50 numbers. Each number is subtracted from 53 and the mean of the numbers so obtained is found to be – 3.5. Find the mean of the given numbers.
Answer.

11. Find the median of the values 37, 31, 42, 43, 46, 25, 39, 45, 32.
Answer. Arranging the data in ascending order, we have 25, 31, 32, 37, 39, 42, 43, 45, 46 Here, number of observations = 9 (odd)

12. If the median of data (arranged in ascending order) 31, 33, 35, x, x+10, 48, 48, 50 is 40, then find value of x.
Answer.

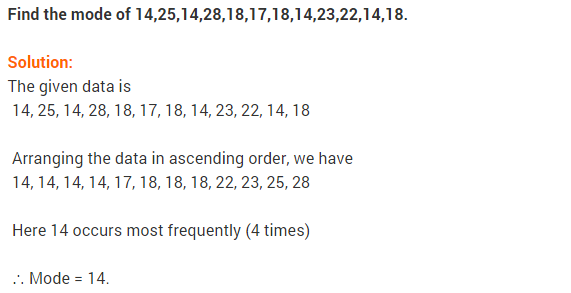
13. Find the mode of the following scores : 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
Answer. 14 repeat maximum number of times (4 times) in the given data.
Mode = 14
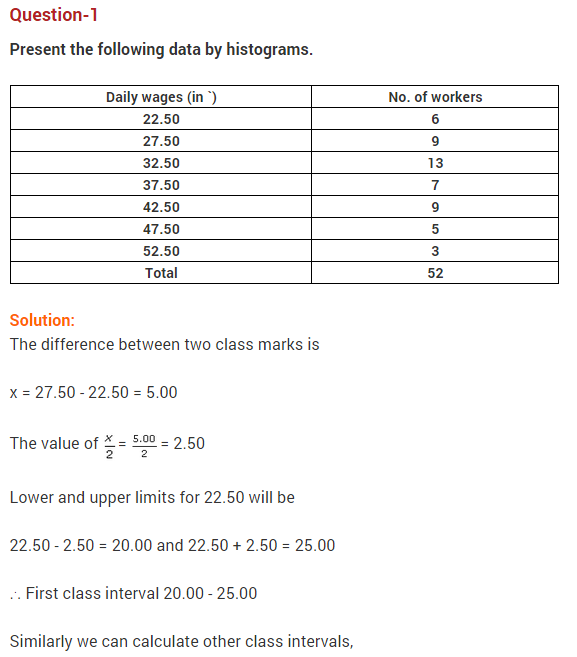
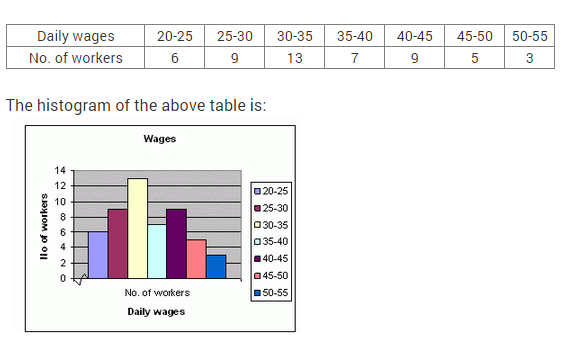
14.To draw a histogram to represent the following frequency distribution :

Find the adjusted frequency for the class 25-45.
Answer.

15. The median of the data 26,56,32,33,60,17,34,29,45 is 33. If 26 is replaced by 62, then find the new median.
Answer. Here, the given data in ascending order is 17, 29, 32, 33, 34, 45, 56, 60, 62

Hence, new median is 34.
SHORT ANSWER QUESTIONS TYPE-I
16. For a particular year, following is the distribution of ages (in years) of primary school teachers in a district:

- Write the lower limit of first class interval.
- Determine the class limits of the fourth class interval.
- Find the class mark of the class 45 – 50.
- Determine the class size. [CBSE March 2012]
Answer.
- First class interval is 15 – 20 and its lower limit is 15.
- Fourth class interval is 30 – 35 Lower limit is 30 and upper limit is 35.
- Class mark of the class 45 – 50 =( 45+50 )/ 2 =95 / 2 =47.5
- Class size = Upper limit of each class interval – Lower limit of each class interval
.•. Here, class size = 20 – 15 = 5
17. The class marks of a frequency distribution are 104, 114, 124, 134, 144, 154, 164. Find the class size and class intervals. [CBSE March 2012]
Answer. Since the class marks are equally spaced.
.•. Class size = 114 – 104 = 10

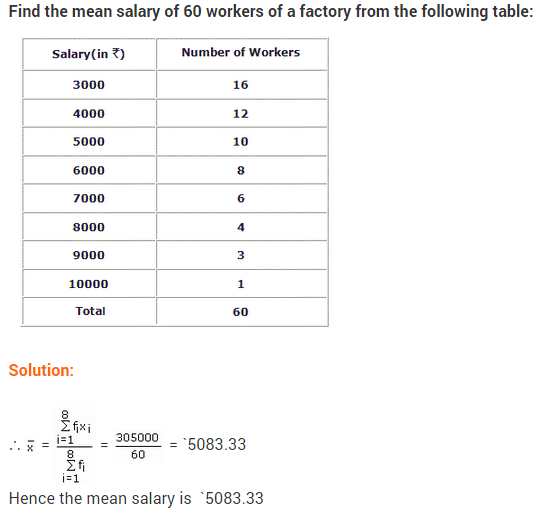
18. Find the mean of the following distribution : [CBSE-14-GDQNI3W]

Answer.

19. The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them in kg are 52, 54, 55, 53, 56, 54. Find the weight of the seventh student. [CBSE March 2012]
Answer.

20. Ten observations 6, 14, 15, 17, x + 1, 2x – 13, 30, 32, 34, 43 are written in ascending order. The median of the data is 24. Find the value of x. [NCERT Exemplar Problem]
Answer. Here, the arranged data is 6, 14, 15, 17, x + 1, 2x – 13, 30, 32, 34, 43
Total number of observations = 10

21. In figure, there is a histogram depicting daily wages of workers in d factory. Construct the frequency distribution table. (CBSE March 2013)

Answer.

22. Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows :
1 6 2 3 5 12 5 8 4 8 10 3 4 12 2
8 15 1 17 6 3 2 5 9 6 8 7 14 12
(i) Make a frequency distribution table for this data, taking class width 5 and one of the class as 5-10.
(ii) How many children watched television for 15 or more than 15 hours a week? [CBSE March 2012]
Answer. (i) Frequency distribution table :

(ii) From the above frequency distribution table, we observe that number of children in the class- interval 15 – 20 is 2.
So, 2 children view television for 15 hours or more than 15 hours a week.
SHORT ANSWER QUESTIONS TYPE-II
23. Given are the scores (out of 25) of 9 students in a Monday test :
14, 25, 17, 22, 20, 19, 10, 8 and 23
Find the mean score and median score of the data. [CBSE-14-GDQNI3W]
Answer.

24. The scores of an English test out of 100 of 20 students are given below :
75, 69, 88, 55, 95, 88, 73, 64, 75, 98, 88, 95, 90, 95, 88, 44, 59, 67, 88, 99.
Find the median and mode of the data [CBSE-14-17DIG1U]
Answer. Ascending order of given data is as given below :
44, 55, 59, 64, 67, 69, 73, 75, 75, 88, 88, 88, 88, 88, 90, 95, 95, 95, 98, 99


25. Obtain the mean of the following distribution and also find the mode. [CBSE-14-ERFKZ8H]

Answer.

LONG ANSWER TYPE QUESTIONS
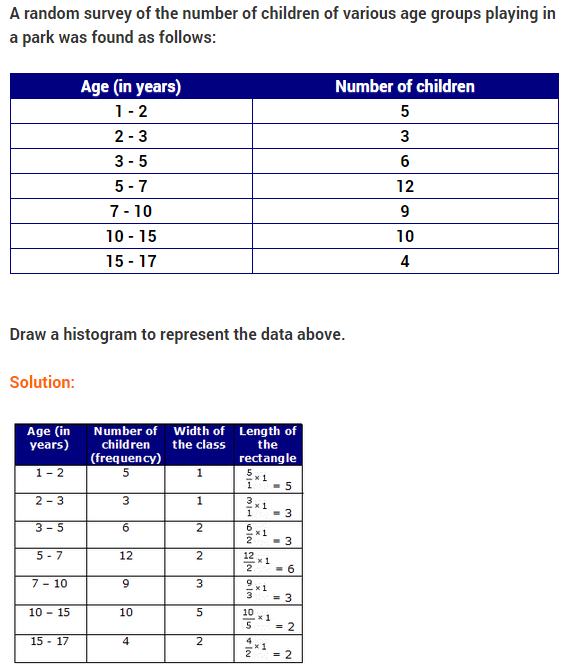
26. A random survey of the number of children of various age groups playing in a park was found as follows :

Draw a histogram to represent the data above.
Answer. In this question, the class sizes are different. So, calculate the adjusted frequency for each class by using the following formula :

Let us represent the class intervals along X-axis and corresponding adjusted frequencies on Y-axis on a suitable scale.
Now, draw rectangles with the class intervals as bases and the corresponding adjusted frequencies as the heights.
Therefore, the required histogram is as given below :

27. In a mathematics test given to 15 students, the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60.
Find the mean, median and mode of this data. [CBSE March 2013]
Answer.


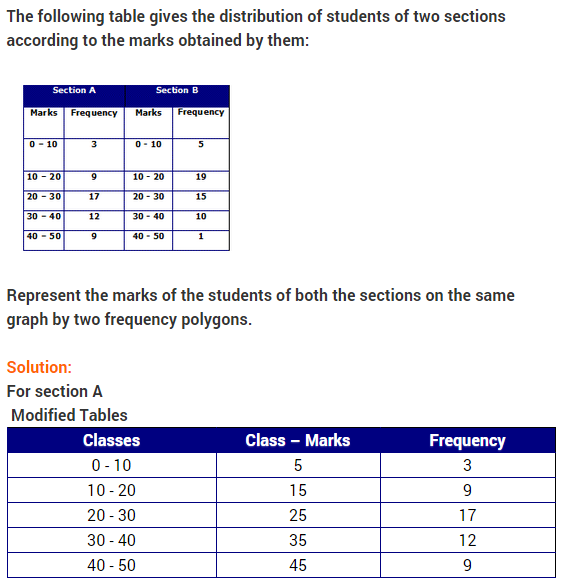
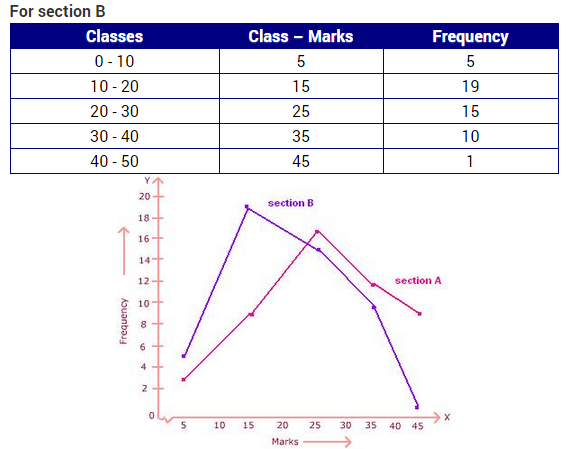
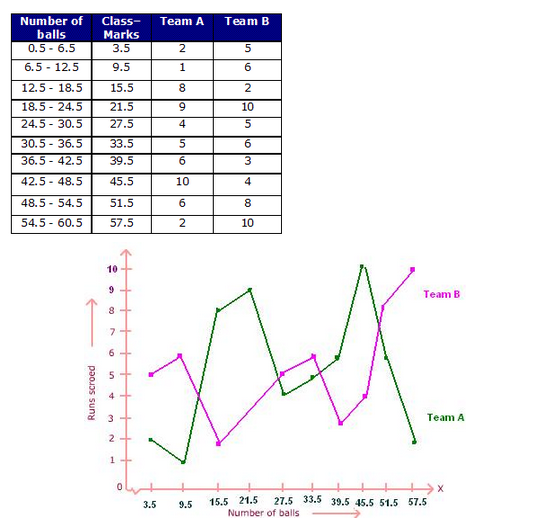
28. The following two tables gives the distribution of students of two sections according to the marks obtained by them : [CBSE March 2011, 2013]

Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer. The class marks are as under :

Let us take class marks on X-axis and frequencies on Y-axis.
To plot frequency polygon of Section-A, we plot the points (5, 3), (15,9), (25,17), (35,12), (45,9) and join these points by line segments.

To plot frequency polygon of Section-B, we plot the points (5,5), (15,19), (25,15), (35,10), (45,1) on the same scale and join these points by dotted line segments.
From the above two polygons, clearly the performance of Section-A is better.
29. The following data given the weight (in grams) of 30 oranges picked from a basket:
106 107 76 109 187 95 125 92 70
139 128 100 88 84 99 113 204 141
136 123 90 115 110 97 90 107 75
80 118 82
Construct a grouped frequency distribution table taking class width equal to 20 in such a way that the mid-value of first class in 70.
From the frequency table, find the number of oranges
(i) weighing more than 180 g.
(ii) less than 100 g. [CBSE-14-GDQNI3W]
Answer. Here , class width = 20
class mark = 70
Half of the class width =20 /2 =10
Upper limit of first class interval = 70 + 10 = 80
Lower limit of first class interval = 70 – 10 = 60
Thus, class interval becomes 60 – 80
So, frequency distribution table becomes :

(a) Number of oranges weights more than 180 g = 1 + 1 = 2
(b) Number of oranges weights less than 100 g = 3 + 10 = 13
30. The following table gives the pocket money (in Rs) given to children per day by their parents : Represent the data in the form of a histogram. [CBSE-14-ERFKZ8H]

Answer. The required histogram is as below :

31. In a school marks obtained by 80 students are given in the table. Draw a histogram. Also, make frequency polygon. [CBSE-14-17DIG1U]

Answer.

32. Draw a histogram and frequency polygon for the following distribution :

Answer. We represent class limits along x-axis and number of students along y-axis on a suitable Scale.

33. Following is the frequency distribution of total marks obtained by the students of different section of class-IX.

Draw a histogram for the distribution.
Answer. Since class intervals of the given frequency distribution are not of equal width.
We would make modifications in the lengths of the rectangles in the histogram, so that the areas of rectangles are proportional to the frequencies.

Now, we draw rectangles with lengths as given in the last column. The histogram of the data is given below :

34. Following table gives the distribution of students of sections A and B of a class according to the marks obtained by them.

Represent the marks of the students of both the sections on the same graph by two frequency polygons. What do you observe ?
Answer.


Value Based Questions
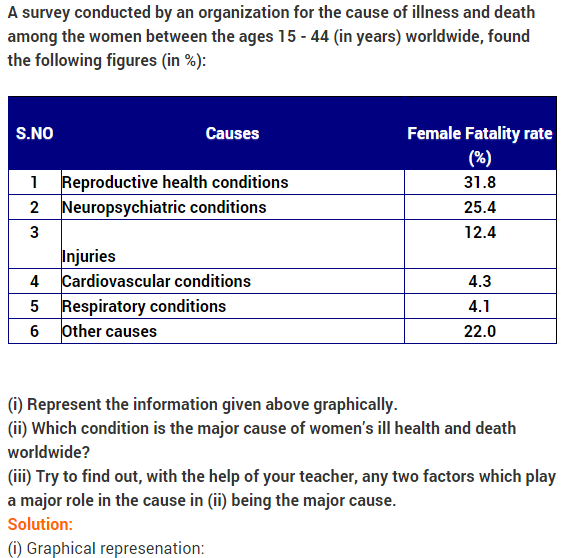
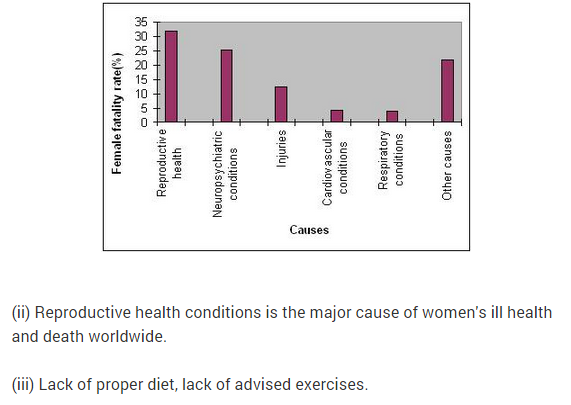
1. A survey conducted by an organisation for the cause of illness and death among the women between the ages 15-44 (in years) worldwide, found the following figures (in %) :

(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
(iii) Try to find out , with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer. (i) The bar graph of the data is as given below :
In the graph, drawn causes of illness and death among women between the ages 15-44 (in years) worldwide is denoted on X-axis and female fatality rate (%) is denoted on the Y-axis.
(ii) The major cause of women’s ill health and death worldwide is reproductive health condition.
(iii) Two other factors which play a major role in the cause in (ii) above are neuro-psychiatric conditions and other causes.

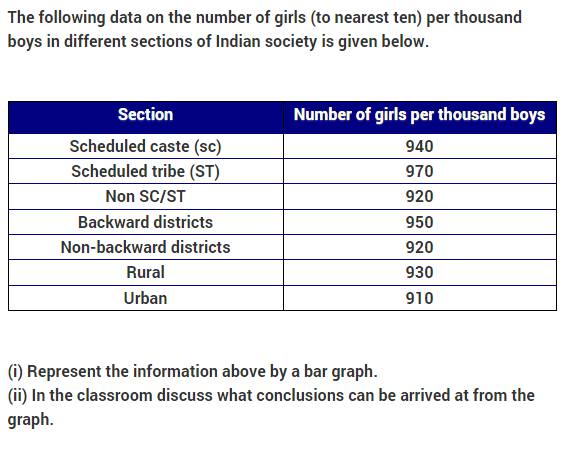
2. The following data on the number of girls (to the nearest ten) per thousand boys in different sections of the Indian society is given below :

(i) Represent the information above by a bar graph.
(ii) In the classroom, discuss what conclusions can be arrived at from the graph.
(iii) What steps should be taken to improve the situation ?
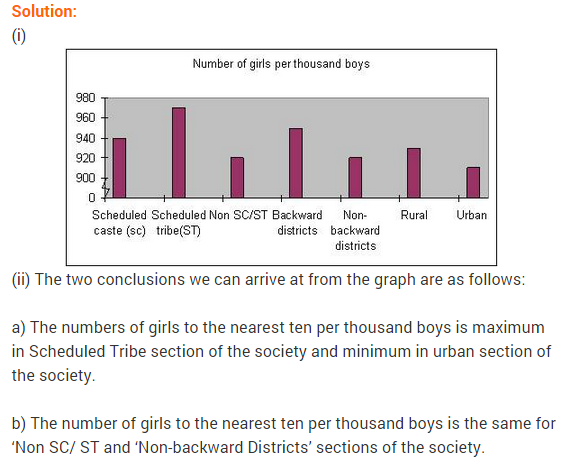
Answer. (i) The required graph is given alongside :
In the graph, different sections of the society is taken on X-axis and number of girls per thousand boys is I taken on the Y-axis. [Scale : 1 cm = 10 girls.]
(ii) From the graph, the number of girls to the nearest ten per i thousand boys are maximum in scheduled tribes whereas they are minimum in urban.
(iii) Prenatal sex determination should strictly banned in urban.

3. Shimpi, a class IX student received cash award of Rs 10000 (Ten thousand) in the singing competition. Her father advised her to make a budget plan for spending this amount. She made the following plan :

Make a bar graph for the above data.
From above answer the following questions :
(i) Which mathematical concepts have been covered in this ?
(ii) How will you rate her budget plan ? In your opinion which head has been given (a) more than deserved and (b) less than it deserved ?
(iii) Which values are depicted in her plan ?
Answer. The bar graph of given data is given below :

In the graph, head is taken on X-axis and amount is taken on Y-axis.
(i) Representation of data using bar graph.
(ii) Very good
(a) Picnic for family
(b) Tuition fee for needy child
(iii) Help the needy people and respect the elders.
4. In a year, the number of deaths due to habit of smoking for different age group is given below :

(i) Represent the given information with the help of a histogram.
(ii) What lesson do you learn from this information ?
Answer. (i) The histogram of given information is as given below :

(ii) Smoking is injurious to health
5. Find the mean of children per family from the data given below :

What values are depicted from this data?
Answer.

