NCERT Solutions for Class 9 Maths Chapter 15 Probability
NCERT Solutions for Class 9 Maths Chapter 15 Probability Ex 15.1
Ex 15.1 Class 9 Maths Question 1.
In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
Here, the total number of trials = 30
∵ Number of times, the ball touched the boundary =6
∴ Number of times, the ball missed the boundary = 30 – 6 = 24
Let the event of not hitting the boundary be represented by E, then

Ex 15.1 Class 9 Maths Question 2.
1500 families with 2 children were selected randomly, and the following data were recorded

Compute the probability of a family, chosen at random, having
(i) 2 girls
(ii) 1 girl
(iii) no girl
Also, check whether the sum of these probabilities is 1.
Solution:
Here, total number of families = 1500
(i) ∵ Number of families having 2 girls = 475
∴ Probability of selecting a family having 2 girls = 475/1500=19/60
(ii) ∵ Number of families having 1 girl = 814
∴ Probability of selecting a family having 1 girl = 814/1500=407/750
(iii) Number of families having no girl = 211
Probability of selecting a family having no girl = 211/1500
Now, the sum of the obtained probabilities
=19/60+407/750+211/1500=475+814+211/1500=1500/1500=1
i.e., Sum of the above probabilities is 1.
Ex 15.1 Class 9 Maths Question 3.
In a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for the data so obtained.
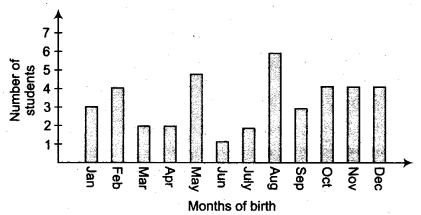
Find the probability that a student of the class was born in August.
Solution:
From the graph, we have
Total number of students bom in various months = 40
Number of students bom in August = 6
∴ Probability of a student of the Class-IX who was bom in August =6/40+3/20
Ex 15.1 Class 9 Maths Question 4.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes.

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution:
Total number of times the three coins are tossed = 200
Number of outcomes in which 2 heads coming up = 72
∴ Probability of 2 heads coming up = 72/200=9/25
∴ Thus, the required probability = 9/25
Ex 15.1 Class 9 Maths Question 5.
An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below.
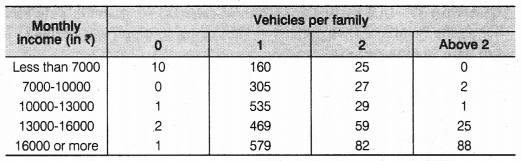
Suppose a family is chosen. Find the probability that the family chosen is
(i) earning ₹ 10000-13000 per month and owning exactly 2 vehicles.
(ii) earning ₹16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹ 7000 per month and does not own any vehicle.
(iv) earning ₹13000-16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Solution:
Here, total number of families = 2400
(i) ∵ Number of families earning Rs. 10000 – Rs. 13000 per month and owning exactly 2 vehicles = 29
∴ Probability of a family earning Rs. 10000 – Rs. 13000 per month and owning exactly 2 vehicles = 29/2400
(ii) ∵ Number of families earning Rs. 16000 or more per month and owning exactly 1 vehicle = 579
∴ Probability of a family earning Rs. 16000 or more per month and owning exactly 1 vehicle = 579/2400
(iii) ∵ Number of families earning less than Rs. 7000 per month and do not own any vehicle = 10
∴ Probability of a family earning less than Rs. 7000 per month and does not own any vehicle = 10/2400 = 1/240
(iv) ∵ Number of families earning Rs. 13000 – Rs. 16000 per month and owning more than 2 vehicles = 25
∴ Probability of a family earning Rs. 13000 – Rs. 16000 per month and owning more than 2 vehicles = 25/2400 = 1/96
(v) ∵ Number of families owning not more than 1 vehicle
= [Number of families having no vehicle] + [Number of families having only 1 vehicle]
= [10 + 1 + 2 + 1] + [160 + 305 + 535 + 469 + 579] = 14 + 2048 = 2062
∴ Probability of a family owning not more than 1 vehicle = 2062/2400 = 1031/1200
Ex 15.1 Class 9 Maths Question 6.
A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. Looking at their performances, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows
0 – 20, 20 – 30, …, 60 – 70, 70 – 100. Then she formed the following table
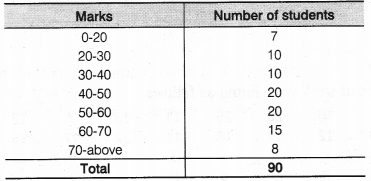
(i) Find the probability that a student obtained less than 20% in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Solution:
Total number of students = 90
(i) From the given table, number of students who obtained less than 20% marks = 7
Probability of a student obtaining less than 20% marks = 7/90
(ii) From the given table, number of students who obtained marks 60 or above = [Number of students in class-interval 60 – 70] + [Number of students in the class interval 70 – above]
= 15 + 8 = 23
∴ Probability of a student who obtained 23 marks 60 or above = 23/90
Ex 15.1 Class 9 Maths Question 7.
To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table

Find the probability that a student chosen at random
(i) likes statistics,
(ii) does not like it.
Solution:
Total number of students whose opinion is obtained = 200
(i) ∵ Number of students who like statistics = 135
∴ Probability of selecting a student who likes statistics = 135/200 = 27/40
(ii) ∵ Number of students who do not like statistics = 65
∴ Probability of selecting a student who does not like statistics = 60/200 = 13/40
Ex 15.1 Class 9 Maths Question 8.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows

What is the empirical probability that an engineer lives
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) within 1/2 km from her place of work?
Solution:
Here, total number of engineers = 40
(i) ∵ Number of engineers who are living less than 7 km from their work place = 9
∴ Probability of an engineer who is living less than 7 km from her place of work = 9/40
(ii) ∵ Number of engineers living at a distance more than or equal to 7 km from their work place = 31
∴ Probability of an engineer who is living at distance more than or equal to 7 km from her place of work = 31/40
(iii) ∵ The number of engineers living within 1/2km from their work place = 0
∴ Probability of an engineer who is living within 1/2km from her place of work = 0/40 = 0
Ex 15.1 Class 9 Maths Question 9.
Activity: Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler?
Solution:
It is an activity. Students can do it themselves.
Ex 15.1 Class 9 Maths Question 10.
Activity : Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digit is divisible by 3.
Solution:
A class room activity for students.
Ex 15.1 Class 9 Maths Question 11.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg)
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
Find the probability that any of these bags,chosen at random contains more than 5 kg of flour.
Solution:
Here, total number of bags = 11
∵ Number of bags having more than 5 kg of flour = 7
∴ Probability of a bag having more than 5 kg of flour = 7/11
Ex 15.1 Class 9 Maths Question 12.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows
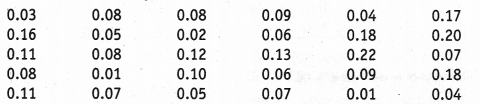
You were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days.
Solution:
Here, total number of days = 30
∵ The number of days on which the sulphur dioxide concentration is in the interval 0.12 – 0.16 = 2
∴ Probability of a day on which sulphur dioxide is in the interval 0.12 – 0.16 = 2/30 = 1/15
Ex 15.1 Class 9 Maths Question 13.
The blood groups of 30 students of class VIII are recorded as follows
A, B, 0, 0, AB, 0, A, 0, B, A, 0, B, A, 0, 0, A, AB, 0, A, A, 0, 0, AB, B, A, B, 0
You were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
Solution:
Here, total number of students = 30
∵ Number of students having blood group AB = 3
∴ Probability of a student whose blood group is AB = 3/30 = 1/10.
Probability Class 9 Extra Questions Maths Chapter 15
Extra Questions for Class 9 Maths Chapter 15 Probability


IMPORTANT QUESTIONS
VERY SHORT ANSWER TYPE QUESTIONS
1. A box contains 50 bolts and 150 nuts. On checking the box, it was found that half of the bolts and half of the nuts are rusted. If one item is chosen at random, find the probability that it is rusted. [CBSE-15-NS72LP7]
Answer.

2. A dice is rolled number of times and its outcomes are recorded as below :

Find the probability of getting an odd number. [CBSE-15-NS72LP7]
Answer. Total number of outcomes = 250
Total number of outcomes of getting odd numbers = 35 + 50 + 53 = 138
.-. P(getting an odd number) = 138/250=69/125
3. IfP (event E) = 0.47, then find P(not E).
Answer. P(not E) = 1 – P(E)
=> 1 – 0.47 = 0.53
4. The probability of guessing the correct answer to a certain question is x/ 2.If probability of not guessing the correct answer is 2 /3 then find x. [CBSE-14-ERFKZ8H], [CBSE-14-17DIG1U]
Answer.

5. A die is thrown six times and number on it is noted as given below :

Compute the probability of getting a prime number. [NCERT Exemplar Problem]
Answer. Here, in 6 trials, each number occur once and total prime numbers i.e., 2, 3, 5 occur one time each
Hence, the number of prime occur = 3
Probability of getting a prime = 3/6 =1/2
6. In a survey of 364 children aged 19-36 months, it was found that 91 liked to eat potato chips. If a child is selected at random, compute the probability that he/she does not like to eat potato chips. [NCERT Exemplar Problem]
Answer. Total children = 364
Number of children like potato chips = 91
.-. Number of children do not like potato chips = 364 – 91 = 273 273
Required probability = 273 / 364 =0.75
7. In a medical examination of students of a class, the following blood groups are recorded :

A student is selected at random from the class. Find the probability that he/she has blood group B. [NCERT Exemplar Problem]
Answer. Total number of students = 10 + 13 + 12 + 5 = 40
Number of students having blood group ‘B’ = 12
Required probability =12 / 40 = 3 / 10
8. Two coins are tossed 1000 times and the outcomes are recorded as below :

Based on this information, find the probability for at most one head.
Answer. Required probability = P(0 heads) + P(1 head)
= 250/1000 + 550 / 1000 = 800/ 1000 =4 / 5 =0.8
9. A bag contains x white, y red and z blue balls. A ball is drawn at the random, then what is the probability of drawing a blue ball.
Answer. Number of blue balls = z
Total balls = x + y + z
therefore P(ablueball)= z /(x+y+z )
10. In a throw of a die, find the probability of not getting 4 or 5.
Answer. Required probability = 1 – P(4) – P(5)
=1- 1 / 6 – 1 / 6 = 4 / 6 = 2 / 3
11. In a sample study of 642 people, it was found that 514 people have a high school certificate. If a person is selected at random, find the probability that the person has a high school certificate.
Answer. Total number of persons = 642
Number of persons with high school certificate = 514
therefore Required probability=514 /642 =0.80
12. In a class, there are x girls and y boys, a student is selected at random, then find the probability of selecting a boy.
Answer. Number of boys = y
Total students = (x + y)
Thus,P(aboy)= y/(x+y)
13. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes ;

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up. [CBSE March 2012]
Answer. Total number of chances = 23 + 72 + 77 + 28 = 200
Number of chances of coming 2 heads = 72
therefore P( coming 2 heads)= 514 / 642 = 9/ 25
SHORT ANSWER QUESTIONS TYPE-I
14. 750 families with 3 children were selected randomly and the following data recorded
If a family member is chosen at random, compute the probability that it has :

(i) no boy child
(ii) no girl child [CBSE-15-6DWMW5A]
Answer. (i) P(no boy child) =100 / 750 = 2/15
(ii) P (no girl child) = 120 /750 =4 /25
15.If the probability of winning a race of an athlete is 1 / 6 less than the twice the probability of losing the race. Find the probability of winning the race. [CBSE-15-6DWMW5A]
Answer. Let probability of winning the race be p Probability of losing the race = 1 – p According to the statement of question, we have
p = 2 (1 – p) – 1/6
=>6p=12-12p-1
=>18p=11
=>p=11 / 18
Hence, probability of winning the race is 11 / 18 .
16. Two coins are tossed simultaneously for 360 times. The number of times ‘2 Tails’ appeared was three times ‘No Tail’ appeared and number of times ‘1 tail’ appeared is double the number of times ‘No Tail’ appeared. Find the probabiliy of getting ‘Two tails’. [CBSE-14-ERFKZ8H], [CBSE-14-17DIG1U]
Answer. Total number of outcomes = 360
Let the number of times ‘No Tail’ appeared be x
Then, number of times ‘2 Tails’ appeared =3x
Number of times ‘1 Tail’ appeared =2x
Now, x + 2x + 3x =360
=>6x=360
=>x=60
P(of getting two tails)=(3 x 60)/360 =1 /2
17. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :

If the three coins are simultaneously tossed again, compute the probability of getting less than 3 tails. [NCERT Exemplar Problem].
Answer. It is given that coin is tossed 200 times Total number of trials = 200
Number of events for getting less than three tails = 68 + 82 + 30 = 180
Probability of getting less than 3 tails =180 / 200 =9 / 10
18. A die was rolled 100 times and the number of times, 6 came up was noted. If the experimental probability calculated from this information is 2 /5 then how many times 6 came up ? Justify your answer. [CBSE March 2013]
Answer.

SHORT ANSWER QUESTIONS TYPE-II
19. The table shows the marks obtained by a student in unit tests out of 50 :

Find the probability that the student get 70% or more in the next unit test. Also, the probability that student get less than 70%. [CBSE-14-GDQNI3W]
Answer.

20. Books are packed in piles each containing 20 books. Thirty five piles were examined for defective books and the results are given in the following table :

One pile was selected at random. What is the probability that it has :
(i) no defective books ?
(ii) more than 0 but less than 4 defective books ?
(iii) more than 4 defective books ? [CBSE-15-NS72LP7]
Answer.

21. The given table shows the month of birth of 40 students of class IX of a particular section in a school.

If one student is chosen at random, find the probability that the student is born :
(a) in the later half of the year
(b) in the month having 31 days
(c) in the month having 30 days [CBSE-14-17DIG1U]
Answer.

22. Two dice are thrown simultaneously 500 times. Each time the sum of two numbers appearing on them is noted and recorded in the following table :

From the above data, what is the probability of getting a sum :
(i) more than 10 (ii) between 8 and 12. [NCERT Exemplar Problem]
Answer.


LONG ANSWER TYPE QUESTIONS
23. The daily cost of milk (in Rs) supplied to 25 houses in a locality are given below :

If one house is chosen at random, find the probability that ;
(a) the milk bill of the house lies between Rs 60 and Rs 80.
(b) house is paying at the most Rs 69, for the milk bill.
(c) the milk bill of the house is below Rs 50. [CBSE-14-ERFKZ8H]
Answer.

24. A travel company has 100 drivers for driving buses to various tourist destination. Given below is a table showing the resting time of the drivers after covering a certain distance (in km).

What is the probability that the driver chosen at random
(a) takes a halt after covering 80 km ?
(b) takes a halt after covering 115 km ?
(c) takes a halt after covering 155 km ?
(d) takes a halt after crossing 200 km ? [CBSE-15-6DWMW5A]
Answer.

25. A survey of 2000 people of different age groups was conducted to find out their preference in watching different types of movies :
Type I —> Family
Type II —> Comedy and Family
Type III —> Romantic, Comedy and Family
Type IV —> Action, Romantic, Comedy and Family

Find the probability that a person chosen at random is :
(a) in 18-29 years of age and likes type II movies
(b) above 50 years of age and likes all types of movies
(c) in 30-50 years and likes type I movies. [CBSE-14-GDQNI3W]
Answer.


Value Based Questions
1. An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table :

Find the probability of the following events for a driver selected at random from the city:
(i) being 18-29 years of age and having exactly 3 accidents in one year.
(ii) being 30-50 years of age and having one or more accidents in a year.
(iii) having no accident in one year.
(iv) Which value would you like to remember from this data ?
Answer.

(iv) Most number of people in India died or injured due to accidents as compared to any other country. So, we should obey the traffic rules as life is very precious.
2.There is a group of 130 people who are patriotic, 50 people believe in violence. What is the probability of people who believe in non-violence 7 Which value you will develop in your character ?
Answer.

In order to have a peaceful environment both values are required patriotism and non-violence. Only patriotism with violence is very dangerous.
3. 100 plants were sown in six different colonies A, B, C, D, E, and E After 31 days, the number of plants survived as follows ;

What is the probability of:
(i) more than 80 plants survived in a colony ?
(ii) less than 82 plants survived in a colony ?
(iii) which value are depicted from above data ?
Answer.

4. For travelling, different mode of transport used by 1500 people are as follows:
Find the probability of number of people :

(i) used car and scooter only ?
(ii) used only cycle ?
(iii) used at least one kind of mode of transport ?
(iv) which value would you learn from above data ?
Answer.

5. There is a group of 75 people who are patriotic, 35 people believe in violence. What is the probability of people who believe in non-violence ? Which value you will develop in your character ?
Answer.

In order, to have a peaceful environment both values are required patriotism and non¬violence. Only patriotism with violence is very dangerous.
