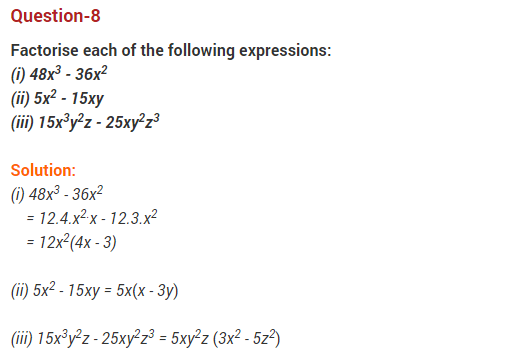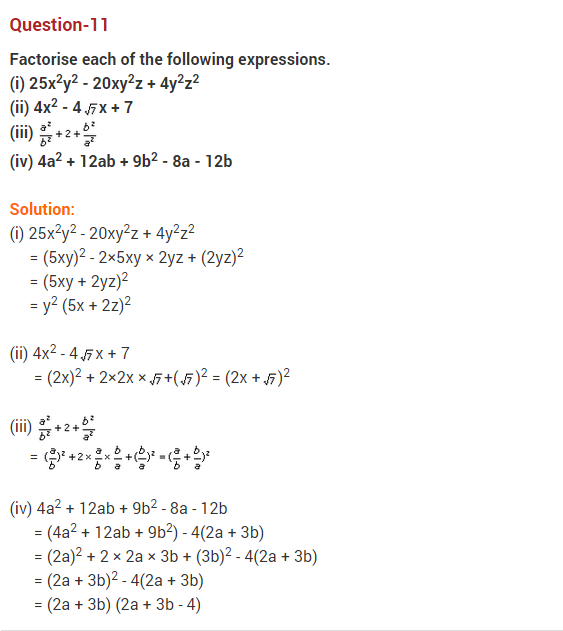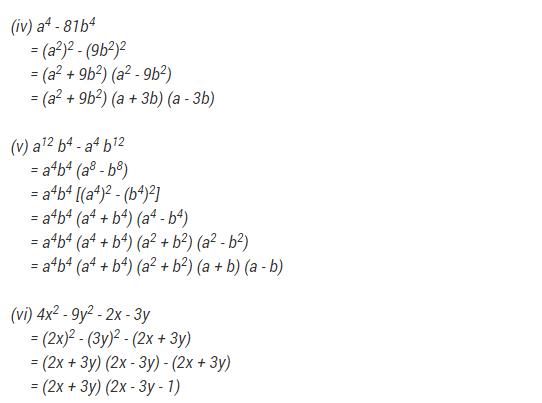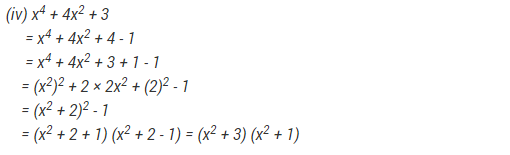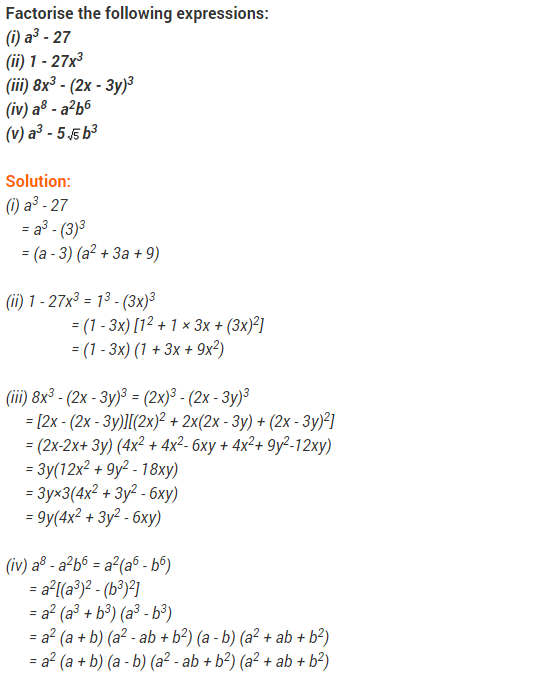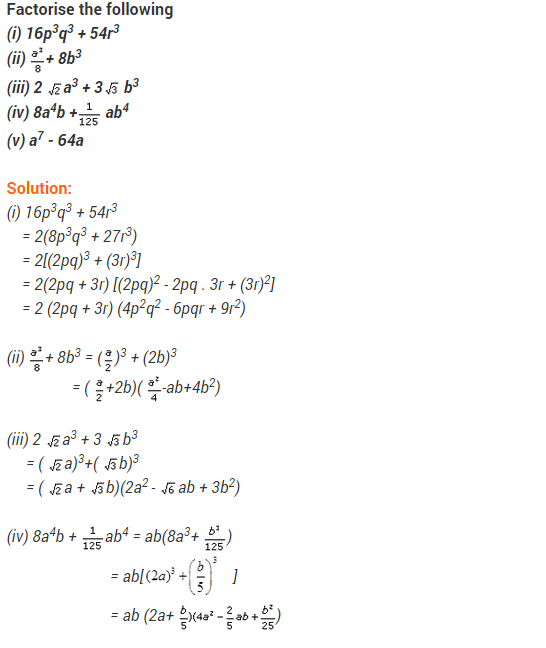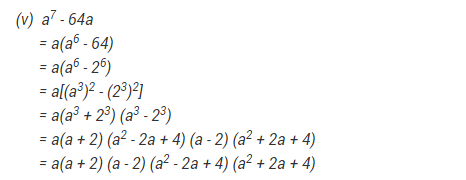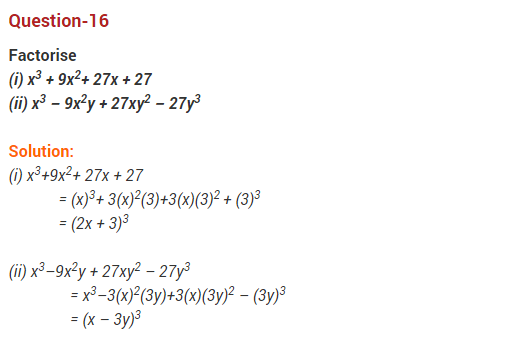NCERT Solutions for Class 9 Maths Chapter 2 Polynomials
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.1
Ex 2.1 Class 9 Maths Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x2 – 3x + 7
(ii) y2 + √2
(iii) 3 √t + t√2
(iv) y+ 2/y
(v) x10+ y3+t50
Solution:
(i) We have 4x2 – 3x + 7 = 4x2 – 3x + 7x0
It is a polynomial in one variable i.e., x
because each exponent of x is a whole number.
(ii) We have y2 + √2 = y2 + √2y0
It is a polynomial in one variable i.e., y
because each exponent of y is a whole number.
(iii) We have 3 √t + t√2 = 3 √t1/2 + √2.t
It is not a polynomial, because one of the exponents of t is 1/2,
which is not a whole number.
(iv) We have y + y+2/y = y + 2.y-1
It is not a polynomial, because one of the exponents of y is -1,
which is not a whole number.
(v) We have x10+ y3 + t50
Here, exponent of every variable is a whole number, but x10 + y3 + t50 is a polynomial in x, y and t, i.e., in three variables.
So, it is not a polynomial in one variable.
Ex 2.1 Class 9 Maths Question 2.
Write the coefficients of x2 in each of the following
(i) 2 + x2 + x
(ii) 2 – x2 + x3
(iii) π/2 x2 + x
(iv) √2 x – 1
Solution:
(i) The given polynomial is 2 + x2 + x.
The coefficient of x2 is 1.
(ii) The given polynomial is 2 – x2 + x3.
The coefficient of x2 is -1.
(iii) The given polynomial is π/2x2 + x.
The coefficient of x2 is π/2.
(iv) The given polynomial is √2 x – 1.
The coefficient of x2 is 0.
Ex 2.1 Class 9 Maths Question 3.
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
(i) Abmomial of degree 35 can be 3x35 -4.
(ii) A monomial of degree 100 can be √2y100.
Ex 2.1 Class 9 Maths Question 4.
Write the degree of each of the following polynomials.
(i) 5x3+4x2 + 7x
(ii) 4 – y2
(iii) 5t – √7
(iv) 3
Solution:
(i) The given polynomial is 5x3 + 4x2 + 7x.
The highest power of the variable x is 3.
So, the degree of the polynomial is 3.
(ii) The given polynomial is 4- y2. The highest
power of the variable y is 2.
So, the degree of the polynomial is 2.
(iii) The given polynomial is 5t – √7 . The highest power of variable t is 1. So, the degree of the polynomial is 1.
(iv) Since, 3 = 3x° [∵ x°=1]
So, the degree of the polynomial is 0.
Ex 2.1 Class 9 Maths Question 5.
Classify the following as linear, quadratic and cubic polynomials.
(i) x2+ x
(ii) x – x3
(iii) y + y2+4
(iv) 1 + x
(v) 3t
(vi) r2
(vii) 7x3
Solution:
(i) The degree of x2 + x is 2. So, it is a quadratic polynomial.
(ii) The degree of x – x3 is 3. So, it is a cubic polynomial.
(iii) The degree of y + y2 + 4 is 2. So, it is a quadratic polynomial.
(iv) The degree of 1 + x is 1. So, it is a linear polynomial.
(v) The degree of 3t is 1. So, it is a linear polynomial.
(vi) The degree of r2 is 2. So, it is a quadratic polynomial.
(vii) The degree of 7x3 is 3. So, it is a cubic polynomial.
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.3
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.4
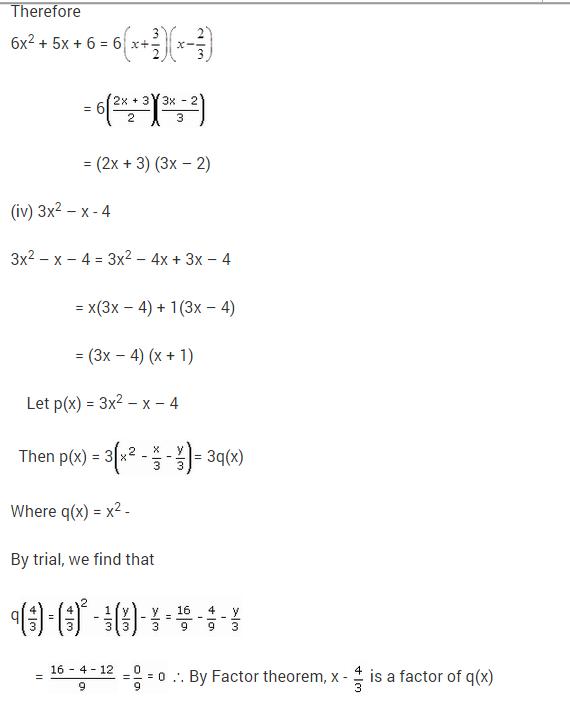
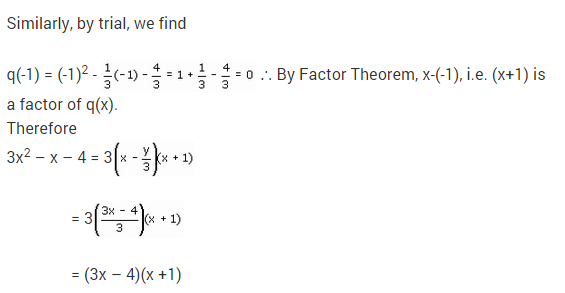
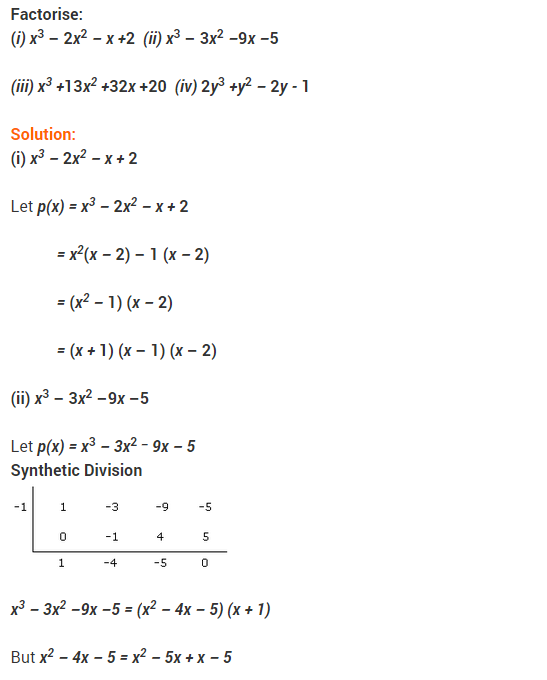
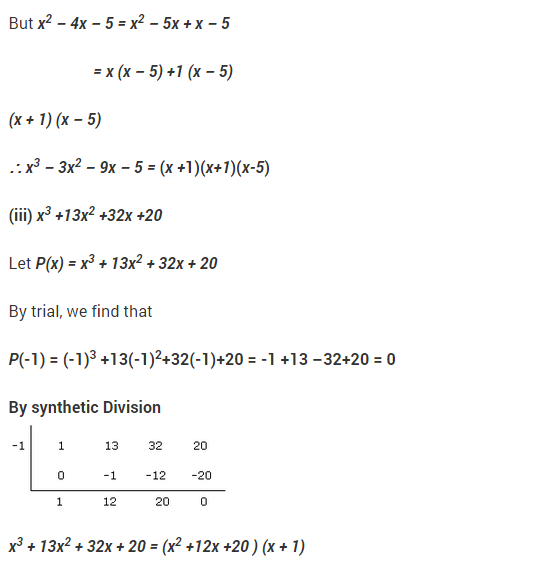
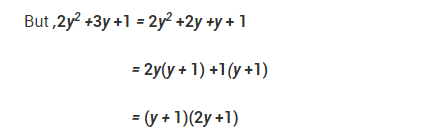
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5
Ex 2.5 Class 9 Maths Question 1
Ex 2.5 Class 9 Maths Question 2
Ex 2.5 Class 9 Maths Question 3
Ex 2.5 Class 9 Maths Question 4
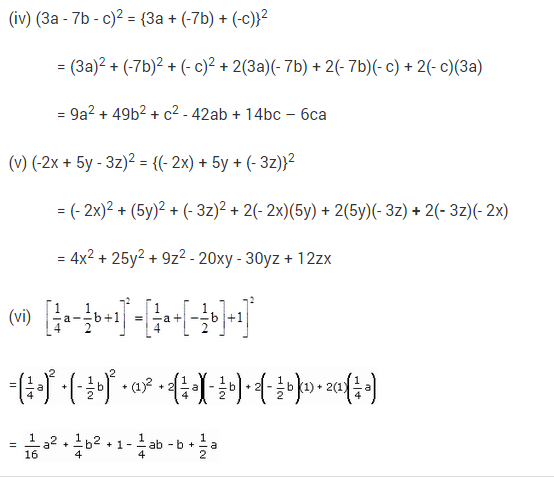
Ex 2.5 Class 9 Maths Question 5
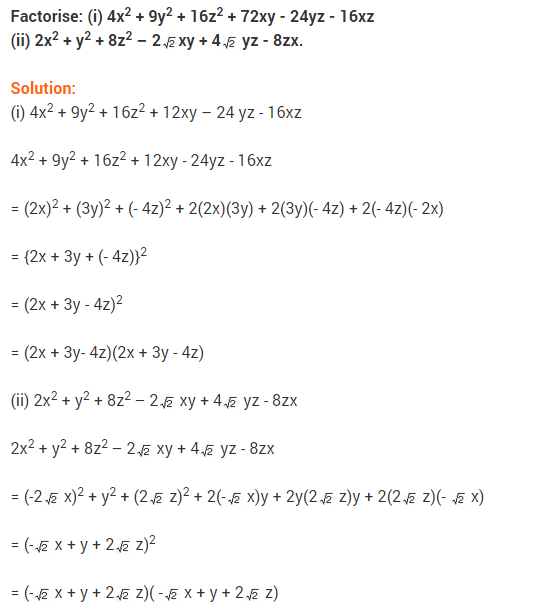
Ex 2.5 Class 9 Maths Question 6
Ex 2.5 Class 9 Maths Question 7
Ex 2.5 Class 9 Maths Question 8
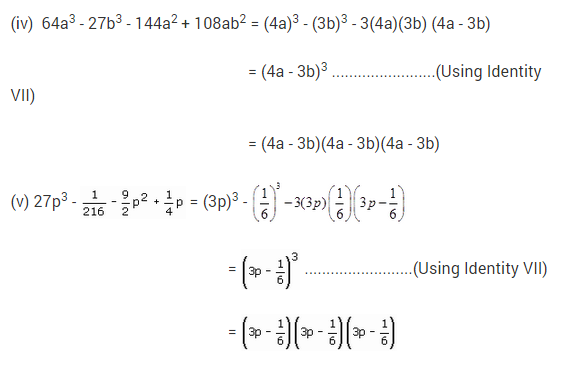
Ex 2.5 Class 9 Maths Question 9
Ex 2.5 Class 9 Maths Question 10
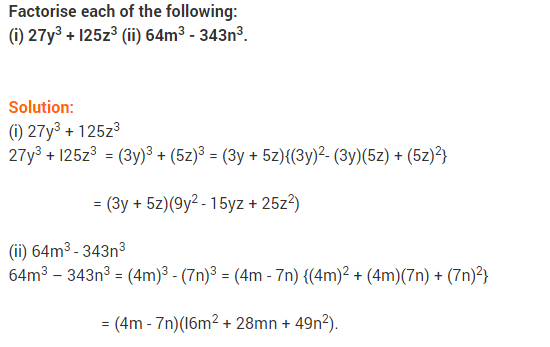
Ex 2.5 Class 9 Maths Question 11
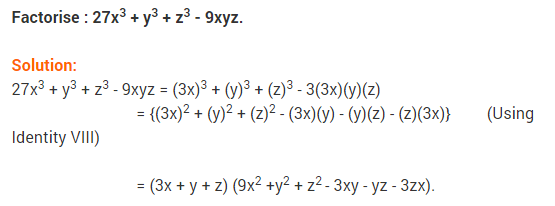
Ex 2.5 Class 9 Maths Question 12
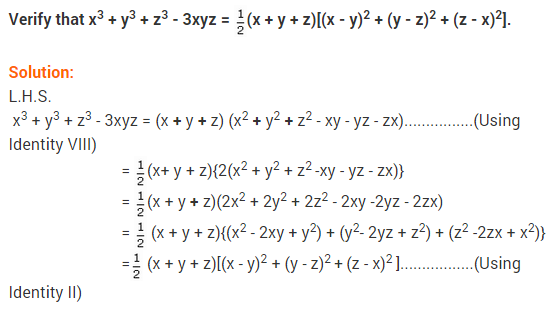
Ex 2.5 Class 9 Maths Question 13
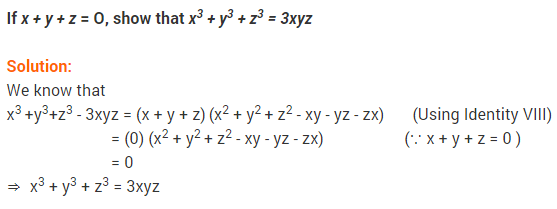
Ex 2.5 Class 9 Maths Question 14
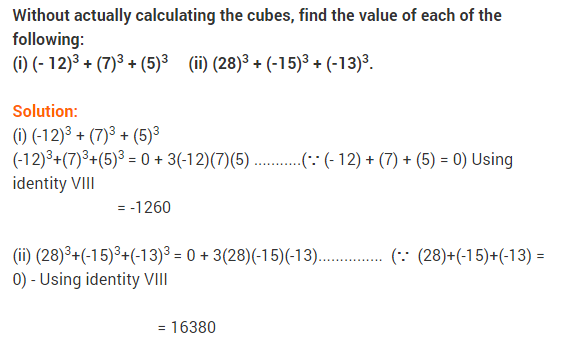
Ex 2.5 Class 9 Maths Question 15
Ex 2.5 Class 9 Maths Question 16
Polynomials Class 9 Extra Questions Maths Chapter 2
Extra Questions for Class 9 Maths Chapter 2 Polynomials
The Complete Educational Website