NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1
Ex 4.1 Class 9 Maths Question 1.
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
(Take the cost of a notebook to be Rs. x and that of a pen to be Rs.y).
Solution:
Let the cost of a notebook = Rs. x
and the cost of a pen = Rs. y
According to the condition, we have
[Cost of a notebook] =2 x [Cost of a pen]
i. e„ (x) = 2 x (y) or, x = 2y
or, x – 2y = 0
Thus, the required linear equation is x – 2y = 0.
Ex 4.1 Class 9 Maths Question 2
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) 2x + 3y = 9.35¯¯¯
(ii) x−y/5−10=0
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = -5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
Solution:
(i) We have 2x + 3y = 9.35¯¯¯
or (2)x + (3)y + (−9.35¯¯¯ ) = 0
Comparing it with ax + by +c= 0, we geta = 2,
b = 3 and c= –9.35¯¯¯ .
(ii) We have x−y5−10=0
or x + (- 1/5) y + (10) = 0
Comparing it with ax + by + c = 0, we get
a =1, b =- 1/5 and c= -10
(iii) Wehave -2x + 3y = 6 or (-2)x + (3)y + (-6) = 0
Comparing it with ax – 4 – by + c = 0,we get a = -2, b = 3 and c = -6.
(iv) We have x = 3y or (1)x + (-3)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 1, b = -3 and c = 0.
(v) We have 2x = -5y or (2)x + (5)y + (0) = 0 Comparing it with ax + by + c = 0, we get a = 2, b = 5 and c = 0.
(vi) We have 3x + 2 = 0 or (3)x + (0)y + (2) = 0 Comparing it with ax + by + c = 0, we get a = 3, b = 0 and c = 2.
(vii) We have y – 2 = 0 or (0)x + (1)y + (-2) = 0 Comparing it with ax + by + c = 0, we get a = 0, b = 1 and c = -2.
(viii) We have 5 = 2x ⇒ 5 – 2x = 0
or -2x + 0y + 5 = 0
or (-2)x + (0)y + (5) = 0
Comparing it with ax + by + c = 0, we get a = -2, b = 0 and c = 5.
NCERT Solutions for Class 9 Maths Linear Equations in Two Variables Ex 4.2

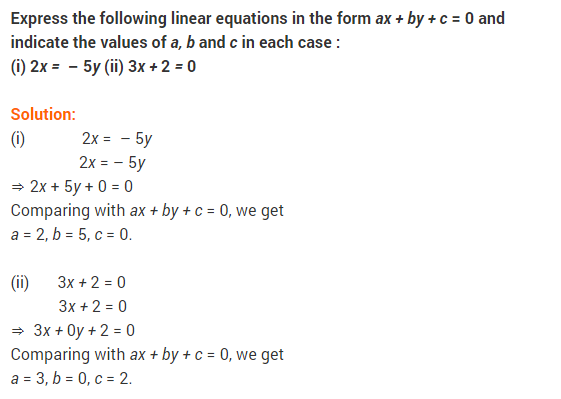
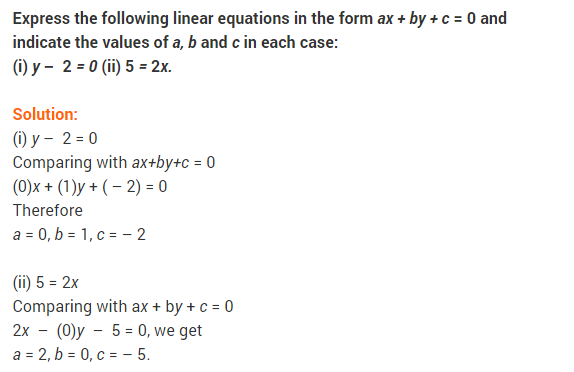



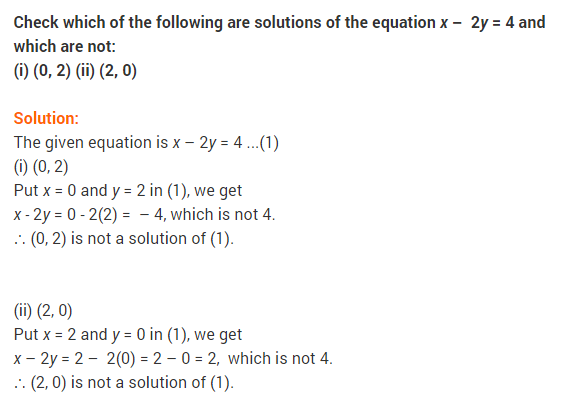

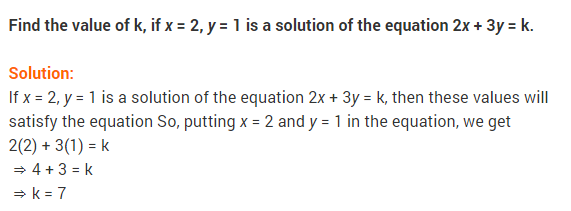


NCERT Solutions for Class 9 Maths Linear Equations in Two Variables Ex 4.3


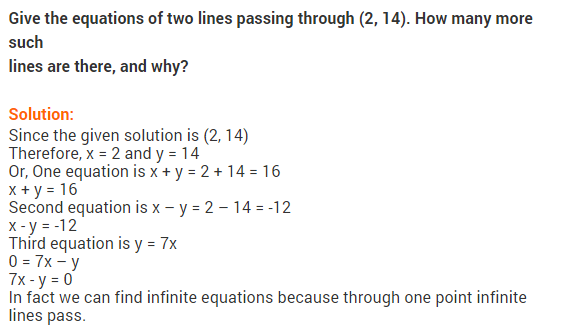
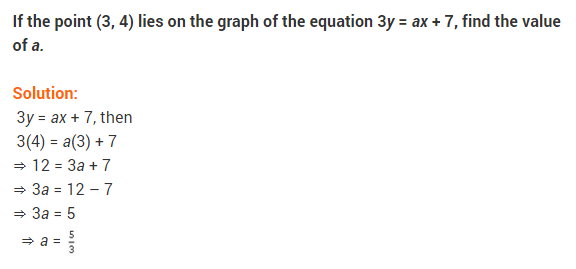








NCERT Solutions for Class 9 Maths Linear Equations in Two Variables Ex 4.4




Linear Equations in Two Variables Class 9 Extra Questions Maths Chapter 4
Extra Questions for Class 9 Maths Chapter 4 Linear Equations in Two Variables





IMPORTANT QUESTIONS
VERY SHORT ANSWER TYPE QUESTIONS
Question.1 Linear equation x – 2 = 0 is parallel to which axis ? [CBSE-15-6DWMW5A]
Solution. Here, linear equation is x-2 = 0 ⇒ x = 2
Thus, it is parallel to y-axis.
Question.2 If (1, -2) is a solution of the equation 2x – y = p, then find the value of p.
Solution.

Question.3 Express x/4 – 3y = – 7 in the form of ax + by + c = 0. [CBSE-15-6DWMW5A]
Solution.

Question. 4 Find the value of k for which x = 0, y — 8 is a solution of 3x – 6y = k. [CBSE-15-NS72LP7]
Solution.

Question .5 Cost of a pen is two and half times the cost of a pencil. Express this situation as a
linear equation in two variables. [CBSE-15-NS72LP7]
Solution.

Question.6 Express x in term of y : x/7 + 2y = 6 [CBSE-14-17DIG1U]
Solution.

Question.7 Find the two solutions of the linear equation 2x – 3y = 12.
Solution.

Question.8 If we multiply or divide both sides of a linear equation with a non-zero number, then what will happen to the solution of the linear equation ? [NCERT Exemplar Problem]
Solution. Solution remains the same.
Question. 9 How many linear equations in x and y can be satisfied by x = 1 and y = 2? [NCERT Exemplar Problem]
Solution. Infinitely many.
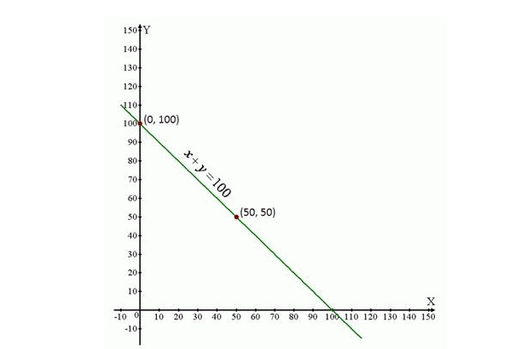
Question.10 In an one day international cricket match, Raina and Dhoni together scored 198 runs. Express the statement as a linear equation in two variables. [CBSE-14-17DIG1U]
Solution. Let runs scored by Raina be x and runs scored by Dhoni be y.
According to statement of the question, we have
x + y = 198
or x + y – 198 = 0
Question.11 Write the equation of a line which is parallel to x-axis and is at a distance of
2 units from the origin. [CBSE-14-ERFKZ8H
Solution. Here, required line is parallel to x-axis and at a distance of 2 units from the origin.
... Its equation is
y + 2= 0 or y-2 = 0
Question.12 Find ‘a’, if linear equation 3x – ay = 6 has one solution as (4, 3).[CBSE -14- ERFKZ8H]
Solution.

Question.13 The cost of a notebook is Rs 5 less than twice the cost of a pen. Write this statement as a linear equation in two variables.
Solution. Let Rs x be the cost of a notebook and Rs y be the cost of a pen, then, we have
x = 2y – 5
⇒ x – 2y + 5 = 0.
Question.14 Total cost of a laptop and a mobile phone is Rs 60000. Write a linear equation in two variables to represent this statement.
Solution. Let the cost price of a laptop be Rs l and cost price of a mobile phone be Rs m.
Since combined cost of a laptop and a mobile phone is Rs 60000 So, l + m = 60000
Question.15 The cost of a table is Rs 100 more than half the cost of a chair. Write this statement as a linear equation in two variables.
Solution.

SHORT ANSWER QUESTIONS TYPE-I
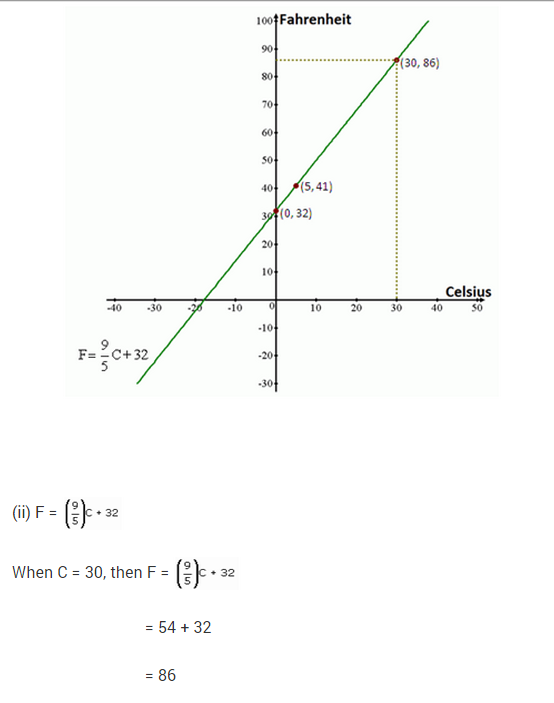
Question.16 In some countries temperature is measured in Fahrenheit, whereas in countries like India it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:
F=[9/5] c+32
If the temperature is – 40°C, then what is the temperature in Fahrenheit ?[CBSE-14-GDQNI3 W]
Solution.

Question.17 Write linear equation representing a line which is parallel to y-axis and is at a distance of 2 units on the left side of y-axis. [CBSE-14-GDQNI3W]
Solution.Here, required equation is parallel to y-axis at a distance of 2 units on the left side of y-axis.
x = – 2 or x + 2 = 0
Question.18 Find the value ofk, if (1, -1) is a solution of the equation 3x-ky = 8. Also, find the coordinates of another point lying on its graph. [CBSE-15-NS72LP7]
Solution.


Question.19 If (p, 2p + 1) is the solution of the linear equation 4x + 3y = 23. Find the value of p.
Solution.

Question.20 Find the value of m, if (5,8) is a solution of the equation 11 x-2y = 3m, then find one more solution of this equation. [CBSE March 2013]
Solution.

Question.21 If π x + 3y = 25, write y in terms of x and also, find the two solutions of this equation. [CBSE-14-17DIG1U]
Solution.

Question.22 Find four solutions of 2x-y = 4. [CBSE March 2011 ]
Solution.


Question.23 Give equation of two lines on same plane which are intersecting at the point (2, 3). [CBSE March 2012]
Solution.
Since there are infinite lines passing through the point (2, 3).
Let, first equation is x + y = 5 and second equation is 2x + 3y = 13
Clearly, the lines represented by both equations intersect at the point (2, 3).
24. Let y varies directly as x. Ify = 12 when x = 4, then write a linear equation. What is the value of y,when x = 5 ? [NCERT Exemplar Problem]
Solution.

Question.25 Give the equations of two lines passing through (2, 14). How many more such lines are there and why ?
Solution.

SHORT ANSWER QUESTIONS TYPE-II
Question.26 Find the value of a for which the equation 2x + ay = 5 has (1, -1) as a solution. Find two more solutions for the equation obtained. [CBSE March 2011 ]
Solution.


Question.27 A fraction becomes 1/4 when 2 is subtracted from the numerator and 3 is added to the denominator. Represent this situation as a linear equation in two variables. Also, find two solutions for this. [CBSE-15-17DIG1U]
Solution. Let numerator and denominator of the given fraction be respectively x and y. According to the statement, we obtain

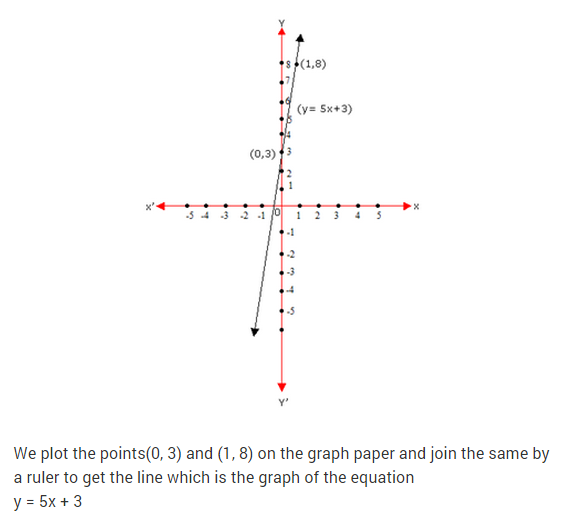
Question.28 Draw the graph of the linear equation y = 2/3 x + 1/3 . Check from the graph that (7, 5)is a solution of the linear equation.
Solution.


Question.29 The cost of two pizzas and 1 burger is Rs 450. Represent this situation algebraically and also, draw the graph. [CBSE-14-ERFKZ8H], [CBSE-15-6DWMW5A]
Solution. Let cost price of one pizza be Rs x and that of one burger be Rs y.
... According to given statement, we have
2x + y = 450
⇒ y = 450 – 2x
When x = 100, y = 250

Question.30 Express y in terms of x for the equation 3x – 4y + 7 = 0. Check whether the points (23, 4) and (0,7/4)lie on the graph of this equation or not.
Solution. Given equation is 3x – 4y + 7 = 0

Question.31 The path of an aeroplane is given by the equation 3x – 4y = 12. Represent the graph graphically. Also, show that the point (- 4, – 6) lies on the graph. [CBSE-15-NS72LP7]
Solution. Given equation is 3x – 4y = 12


Question.32 Rupinder and Deepak two students of a vidyalaya contribute to charity. The Contribution of Rupinder is 2/5 of the contribution of Deepak. Write a linear equation According to the above statement and draw the graph for the linear equation.
Solution.

Question.33 Draw the graph of the equation y = mx + c for m = 3 and c = – 1 (a straight line in Cartesian plane). Read from the graph the value of when x = 2.
Solution.

Question.34 The following observed values of x Write the linear equation :
Draw the graph using the values of x, graph of the linear equation.

(i) cuts the x-axis (ii) cuts the y-axis
Solution.


LONG ANSWER TYPE QUESTIONS
Question.35 On the graph paper draw the straight line 3x – 2y = 4 and x + y – 3 = 0. Also, find their point of intersection on the graph.
Solution. The two given equations are


Question.36 If (2,3) and (4, 0) lie on the graph of equation ax + by = 1. Find the value of a and b. Plot the graph of equation obtained. [CBSE March 2012]
Solution.


Question.37 Draw the graphs of the following equations on the same graph sheet: x = 4,x = 2,y = l and y – 3 = 0
Solution.

Question.38 Write the equations of the lines drawn in following graph :

Solution.

Question.39 Represent 2x + 3y = 6 by a graph. Write the coordinates of the point where it meets: (a) x-axis (b) y-axis [CBSE-14-GDQNI3W]
Solution.

Question.40 You know that the force applied on a body is directly proportional to the acceleration produced in the body. Write an equation to express this situation and plot the graph of the equation, taking constant as 5, force on y-axis and acceleration on x-axis. Also, find acceleration produced in a body, if force applied on it is 20 units. [CBSE-14-ERFKZ8H]
Solution. Let x be the acceleration produced in the body on application of a force of y units. According to the statement of the question. We have y = kx, where k is a constant.

Question.41 Cost of 1 pen is Rs x and that of 1 pencil is Rs y. Cost of 2 pens and 3 pencils together is Rs 18. Write a linear equation which satisfies this data. Draw the graph for the same. [CBSE- 14ERFKZ8H]
Solution.


Plot the points (0, 6), (3, 4) and (9, 0). Join them in pairs to get the required line.
Question.42 Sum of two numbers is 8. Write this in the form of a linear equation in two variables. Also, draw the line given by this equation. Find graphically the numbers, if difference between them is 2. [CBSE-15-6DWMW5A]
Solution.



Value Based Questions (Solved)
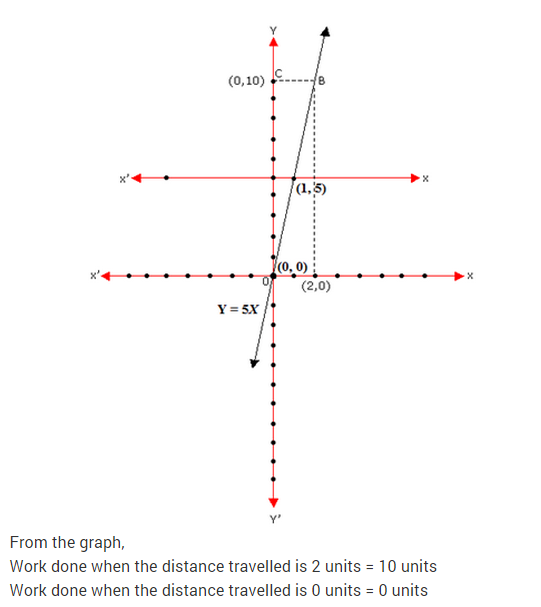
Question.1 If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units. Also, read from the graph the work done when the distance travelled by the body is :
(i) 2 units (ii) 0 unit.
(iii) In context of values, if work done relates with ‘Hard work’ and ‘Knowledge’ relates with ‘key’ then what will one achieve ?
Solution. Let the work done by constant force be y units and the distance travelled by the body be x units. Since the work done by a body on application of a constant force (F) is directly proportional to the distance travelled by the body.
It can be expressed in the form of a linear equation in two variables is as

Now, we have to draw the graph by taking the constant force as 5 units.
From equation (i), we have
From graph:
- When the distance travelled is 2 units, then the work done is 10 units.
- When the distance travelled is 0 unit, then the work done is also 0 unit.
- Success
Question.2 Lipsa and Mona are two students of IX class of DAV school. Together they contributed? 100 towards the old age home to help the old persons.
(i) Write a linear equation which satisfies the given data and draw the graph.
(ii)What values are depicted in their plan?
Solution.



Question.3 Mrs Sharma lost her purse containing 50 rupee and 100 rupee notes amount to Rs 1500 in a shop. Next day shopkeeper found the purse during dusting. He immediately went to Mrs Sharma’s house and returned the purse and rupees. Mrs Sharma appreciates the shopkeeper for his act. ‘
(i) Represent the situation as an equation and draw the graph.
(ii)What value do you learn from shopkeeper’s act ?
Solution.



Question.4 In an election, a good candidate may lose because 40% of voters do not cast their votes due to various reasons. Form an equation and draw the graph with data. From the graph, find:
(i) The total number of voters, if 720 voters cast their votes.
(ii)The number of votes cast, if the total number of voters are 1000.
(iii) What message did you get from above information?
Solution.


From the graph, we see that:
(i) When total votes polled = 720 i.e., y = 720, the total number of voters i.e., x = 1200 Hence, total number of voters = 1200.
(ii)When total number of voters x = 1000 Number of votes cast is 600.
(iii) Every voters should cast vote to elect an honest candidate.
